如图，在四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，侧棱 $A{A_1} \perp 底面ABCD$，$AB\parallel DC$，$A{A_1} = 1$，$AB = 3k$，$AD = 4k$，$BC = 5k$，$DC = 6k\left(k > 0\right)$．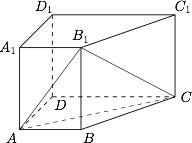
【难度】
【出处】
2013年高考福建卷（理）
【标注】
-
求证：$CD \perp 平面 AD{D_1}{A_1}$；标注答案略解析在平面 $ADD_1A_1$ 中，找到两条均与 $CD$ 垂直的相交直线即可．取 $CD$ 的中点 $E$，连接 $BE$．如图．
因为 $AB\parallel DE$，$AB = DE = 3k$，所以四边形 $ABED$ 为平行四边形，所以 $BE\parallel AD$ 且\[BE = AD = 4k.\]在 $\triangle BCE$ 中，$BE = 4k$，$CE = 3k$，$BC = 5k$，所以\[B{E^2} + C{E^2} = B{C^2},\]所以 $\angle BEC = 90^\circ $，即 $BE \perp CD$．
因为 $BE\parallel AD$，所以 $CD \perp AD$．
因为 $A{A_1} \perp 平面 ABCD$，$CD \subset 平面 ABCD$，
因为 $A{A_1} \perp CD$，又 $A{A_1} \cap AD = A$，
$\therefore$ $CD \perp 平面 AD{D_1}{A_1}$． -
若直线 $A{A_1}$ 与平面 $A{B_1}C$ 所成角的正弦值为 $\dfrac{6}{7}$，求 $k$ 的值；标注答案$1$解析建立空间直角坐标系，利用向量法求出线面角即可．可用向量法解决线面所成角问题．
以 $D$ 为原点，$\overrightarrow {DA}$，$\overrightarrow {DC} $，${\overrightarrow {DD} _1}$ 的方向为 $x$，$y$，$z$ 轴的正方向建立如图 2 所示的空间直角坐标系，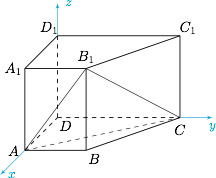
则\[A\left( {4k,0,0} \right),C\left( {0,6k,0} \right),{B_1}\left( {4k,3k,1} \right),{A_1}\left( {4k,0,1} \right),\]所以\[\begin{split}\overrightarrow {AC} & = \left( { - 4k,6k,0} \right), \\ \overrightarrow {A{B_1}} & = \left( {0,3k,1} \right), \\ \overrightarrow {A{A_1}} & = \left( {0,0,1} \right).\end{split}\]设平面 $A{B_1}C$ 的法向量 $\overrightarrow n = \left( {x,y,z} \right)$，则由\[{\begin{cases}\overrightarrow {AC} \cdot \overrightarrow n = 0, \\
\overrightarrow {A{B_1}} \cdot \overrightarrow n = 0, \\
\end{cases}}\]得\[{\begin{cases}- 4kx + 6ky = 0, \\
3ky + z = 0 .\\
\end{cases}}\]取 $y = 2$，得\[\overrightarrow n = \left( {3,2, - 6k} \right).\]设 $A{A_1}$ 与平面 $A{B_1}C$ 所成角为 $\theta $，则\[\begin{split} \sin \theta &= \left| {\cos \left\langle {\overrightarrow {A{A_1}} ,} \right.\left. {\overrightarrow n } \right\rangle } \right| \\ & = \left| {\dfrac{{\overrightarrow {A{A_1}} \cdot \overrightarrow n }}{{\left| {\overrightarrow {A{A_1}} } \right|\left| {\overrightarrow n } \right|}}} \right| \\ & = \dfrac{6k}{{\sqrt {36{k^2} + 13} }} = \dfrac{6}{7},\end{split} \]解得\[k = 1,\]故所求 $k$ 的值为 $1$． -
现将与四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为 $f\left( k \right)$，写出 $f\left( k \right)$ 的解析式．（直接写出答案，不必说明理由）标注答案共有 $ 4 $ 种不同的方案．\[f\left(k\right)={\begin{cases}
72{k^2} + 26k,0 < k \leqslant \dfrac{5}{18}, \\
36{k^2} + 36k,k > \dfrac{5}{18}. \\
\end{cases}}\]解析注意要拼成新的四棱柱，需满足拼接后不会增加多余的面，并且符合凸多面体的要求．共有 $ 4 $ 种不同的方案．\[f\left(k\right)={\begin{cases}
72{k^2} + 26k,0 < k \leqslant \dfrac{5}{18}, \\
36{k^2} + 36k,k > \dfrac{5}{18}. \\
\end{cases}}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
