如图,已知椭圆 $C_1:\frac{x^2}{2}+y^2=1$,抛物线 $C_2:y^2=2px(p>0)$,点 $A$ 是椭圆 $C_1$ 与抛物线 $C_2$ 的交点.过点 $A$ 的直线 $l$ 交椭圆 $C_1$ 于点 $B$,交抛物线 $C_2$ 与点 $M$($B、M$ 不同于 $A$).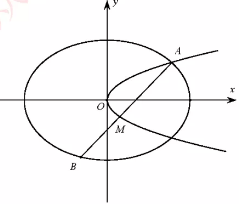

【难度】
【出处】
2020年高考浙江卷
【标注】
-
若 $p=\frac{1}{16}$,求抛物线 $C_2$ 的焦点坐标;标注答案$\left(\frac{1}{32},0\right)$解析略
-
若存在不过原点的直线 $l$ 使 $M$ 是线段 $AB$ 的中点,求 $p$ 的最大值.标注答案略解析设 $A\left(x_1,y_1\right)$,$M\left(x_2,y_2\right)$.
其中 $y_i^2=2px_i$,$i=1,2$.
由 $k_{OM}k_{AB}=-\frac12$,列方程 $\frac{y_2}{x_2}\cdot\frac{y_2-y_1}{x_2-x_1}=-\frac12$.
整理可得 $y_2\left(y_2+y_1\right)+8p^2=0$.关于 $y_2$ 的二次方程在 $\left[-y_1,0\right]$ 中有解,可以解得 $y_1^2\geqslant 32p^2$.
则 $x_1\geqslant 16p$.
将椭圆和抛物线联立可得 $x^2+4px-2=0$,其正根要不小于 $16p$,解得 $160p^2\leqslant 1$.
即 $0<p<\frac{1}{4\sqrt{10}}$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2