某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底 $O$ 在水平线 $MN$ 上,桥 $AB$ 与 $MN$ 平行,$OO'$ 为铅垂线($O'$ 在 $AB$ 上).经测量,左侧曲线 $AO$ 上任一点 $D$ 到 $MN$ 的距离 $h_1$(米)与 $D$ 到 $OO'$ 的距离 $a$(米)之间满足关系式 $h_1=\frac{1}{40}a^2$;右侧曲线 $BO$ 上任一点 $F$ 到 $MN$ 的距离 $h_2$(米)与 $F$ 到 $OO'$ 的距离 $b$(米)之间满足关系式 $h_2=-\frac{1}{800}b^3+6b$.已知点 $B$ 到 $OO'$ 的距离为 $40$ 米.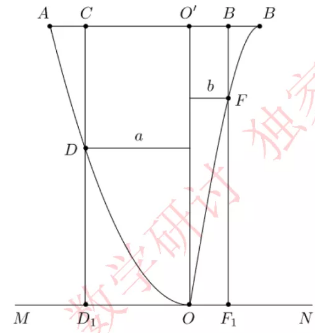

【难度】
【出处】
2020年高考江苏卷
【标注】
-
求桥 $AB$ 的长度;标注答案$120$(米)解析解:设 $AA_1,BB_1,CD_1,EF_1$ 都与 $MN$ 垂直,$A_1,B_1,D_1,F_1$ 是相应垂足.
由条件知,当 $O'B=40$ 时,
$BB_1=-\frac{1}{800}\times40^3+6\times40=160$,则 $AA_1=160.$
由 $\frac{1}{40}O'A^2=160$,得 $O'A=80.$
所以 $AB=O'A+O'B=80+40=120$(米). -
计划在谷底两侧建造平行于 $OO'$ 的桥墩 $CD$ 和 $EF$,且 $CE$ 为 $80$ 米,其中 $C,E$ 在 $AB$ 上(不包括端点).桥墩 $EF$ 每米造价 $k$(万元),桥墩 $CD$ 每米造价 $\frac{3}{2}k$(万元)$(k>0)$,问 $EF,O'E$ 为多少米时,桥墩 $CD$ 与 $EF$ 的总造价最低?标注答案$20$ 米解析以 $O$ 为原点,$OO'$ 为 $y$ 轴建立平面直角坐标系 $xOy$(如图所示).
设 $F(x,y_2),x\in(0,40)$,则 $y_2=-\frac{1}{800}x^3+6x$,
$EF=160-y_2=160+\frac{1}{800}x^3-6x.$
因为 $CE=80$,所以 $O'C=80-x.$
设 $D(x-80,y_1)$,则 $y_1=\frac{1}{40}(80-x)^2$,
所以 $CD=160-y_1=160-\frac{1}{40}(80-x)^2=-\frac{1}{40}x^2+4x.$
记桥墩 $CD$ 和 $EF$ 的总造价为 $f(x)$,
则 $f(x)=k(160+\frac{1}{800}x^3-6x)+\frac{3}{2}k(-\frac{1}{40}x^2+4x)$
$=k(\frac{1}{800}x^2-\frac{3}{80}x^2+160)(0<x<40).$
$f'(x)=k(\frac{3}{800}x^3-\frac{3}{40}x)=\frac{3k}{800}x(x-20)$,
令 $f'(x)=0$,得 $x=20$.$$\begin{array}{|c|c|c|c|}\hline x & (0,20) & 20 & (20,40) \\ \hline f'(x) & - & 0 & + \\ \hline f(x) & \searrow & \text{极小值} & \nearrow \\ \hline \end{array}$$所以当 $x=20$ 时,$f(x)$ 取得最小值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2