某学生兴趣小组随机调查了某市 $100$ 天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：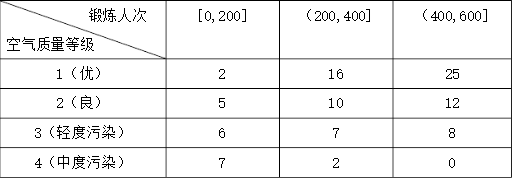
附：$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$$，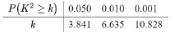
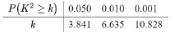
附：$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$$，【难度】
【出处】
2020高考全国（Ⅲ）卷（理）
【标注】
-
分别估计该市一天的空气质量等级为 $1,2,3,4$ 的概率；标注答案略解析解：由所给数据，该市一天的空气质量等级为 $1,2,3,4$ 的概率的估计值如下表：$$\begin{array}{|c|c|c|c|c|}\hline \text{空气质量等级} & 1 & 2 & 3 & 4 \\ \hline \text{概率的估计值} & 0.43 & 0.27 & 0.21 & 0.09 \\ \hline \end{array}$$
-
求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；标注答案$350$解析解：一天中到该公园锻炼的平均人次的估计值为$$\frac{1}{100}(100\times20+300\times35+500\times45)=350.$$
-
若某天的空气质量等级为 $1$ 或 $2$，则称这天“空气质量好”；若某天的空气质量等级为 $3$ 或 $4$，则称这天“空气质量不好”。根据所给数据，完成下面的 $2\times2$ 列联表，并根据列联表，判断是否有 $95\%$ 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？
标注答案有把握解析解：根据所给数据，可得 $2\times2$ 列联表：$$\begin{array}{|c|c|c|} \hline & \text{人次}\leqslant 400 & \text{人次}\geqslant 400 \\ \hline \text{空气质量好} & 33 & 37 \\ \hline \text{空气质量不好} & 22 & 8 \\ \hline \end{array}$$根据列联表得$$K^2=\frac{100\times(33\times8-22\times37)^2}{55\times45\times70\times30}\approx5.820.$$由于 $5.820>3.841$，故有 $95\%$ 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
