如图，在长方体 $ABCD-A_1B_1C_1D_1$ 中，点 $E,F$ 分别在棱 $DD_1,BB_1$ 上，且 $2DE=ED_1,BF=2FB_1$．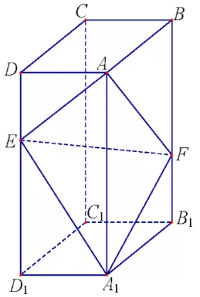
【难度】
【出处】
2020高考全国（Ⅲ）卷（理）
【标注】
-
证明：点 $C_1$ 在平面 $AEF$ 内；标注答案略解析解：设 $AB=a,AD=b,AA_1=c$，如图，以 $C_1$ 为坐标原点，$\overrightarrow{C_1D_1}$ 的方向为 $x$ 轴正方向，建立空间直角坐标系 $C_1-xyz.$
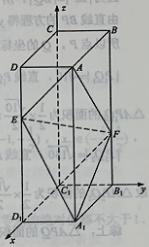连结 $C_1F$，则 $C_1(0,0,0),A(a,b,c),E(a,0,\frac{2}{3}c),F(0,b,\frac{1}{3}c),\overrightarrow{EA}=(0,b,\frac{1}{3}c),\overrightarrow{C_1F}=(0,b,\frac{1}{3}c)$，得$$\overrightarrow{EA}=\overrightarrow{C_1F},$$因此 $EA\parallel C_1F$，即 $A,E,F,C_1$ 四点公面，所以点 $C_1$ 在平面 $AEF$ 内． -
若 $AB=2,AD=1,AA_1=3$，求二面角 $A-EF-A_1$ 的正弦值．标注答案$\frac{\sqrt{42}}{7}$解析解：由已知得 $A(2,1,3),E(2,0,2),F(0,1,1),A_1(2,1,0),\overrightarrow{AE}=(0,-1,-1),\overrightarrow{AF}=(-2,0,-2),\overrightarrow{A_1E}=(0,-1,2),\overrightarrow{A_1F}=(-2,0,1).$
设 $\boldsymbol{n_1}=(x,y,z)$ 为平面 $AEF$ 的法向量，则
$\begin{cases}\boldsymbol{n_1}\cdot\overrightarrow{AE}=0,\\\boldsymbol{n_1}\cdot\overrightarrow{AF}=0,\end{cases}$，即 $\begin{cases}-y-z=0,\\-2x-2z=0,\end{cases}$ 可取 $\boldsymbol{n_1}=(-1,-1,1).$
设 $\boldsymbol{n_2})$ 为平面 $A_1EF$ 的法向量，则
$\begin{cases}\boldsymbol{n_2}\cdot\overrightarrow{A_1E}=0,\\\boldsymbol{n_2}\cdot\overrightarrow{A_1F}=0,\end{cases}$ 同理可取 $\boldsymbol{n_2}=(\frac{1}{2},2,1).$
因为 $\cos<\boldsymbol{n_1},\boldsymbol{n_2}>=\frac{\boldsymbol{n_1}\cdot\boldsymbol{n_2}}{|\boldsymbol{n_1}||\boldsymbol{n_2}|} =-\frac{\sqrt7}{7} $，所以二面角 $ A-EF-A_1 $ 的正弦值为 $ \frac{\sqrt{42}}{7}.$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
