已知函数 $f(x)=|3x+1|-2|x-1|.$
【难度】
【出处】
2020高考全国（Ⅰ）卷（理）
【标注】
-
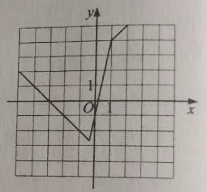
画出 $y=f(x)$ 的图像；标注答案
解析解：由题设知
$f(x)=\begin{cases}-x-3,&&x\leqslant -\frac{1}{3},\\5x-1.&&-\frac{1}{3}<x\leqslant 1,\\x+3,&&x>1.\end{cases}$
$y=f(x)$ 的图像如图所示． -
求不等式 $f(x)>f(x+1)$ 的解集．标注答案$(-\infty,-\frac{7}{6})$解析解：函数 $y=f(x)$ 的图像向左平移 $1$ 个单位长度后得到函数 $y=f(x+1)$ 的图像．
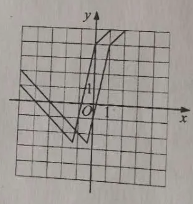$y=f(x)$ 的图像与 $y=f(x+1)$ 的图像的焦点坐标为 $(-\frac{7}{6},-\frac{11}{6})$．
由图像可知当且仅当 $x<-\frac{7}{6}$ 时，$y=f(x)$ 的图像在 $y=f(x+1)$ 的图像上方，
故不等式 $f(x)>f(x+1)$ 的解集为 $(-\infty,-\frac{7}{6})$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
