某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二。为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表: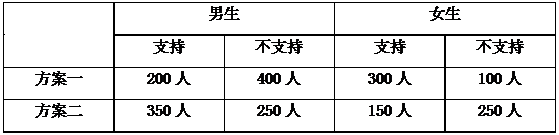 假设所有学生对活动方案是否支持相互独立。
假设所有学生对活动方案是否支持相互独立。
 假设所有学生对活动方案是否支持相互独立。
假设所有学生对活动方案是否支持相互独立。【难度】
【出处】
2020年高考北京卷
【标注】
-
分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;标注答案$\frac{1}{3};\frac{3}{4}$解析解:设“该校男生支持方案一”为事件 $A$,“该校女生支持方案以”为事件 $B$,
则 $P(A)=\frac{200}{200+400}=\frac{1}{3},P(B)=\frac{300}{300+100}=\frac{3}{4}$. -
从该校全体男生中随机抽取 $2$ 人,全体女生中随机抽取 $1$ 人,估计这 $3$ 人中恰有 $2$ 人支持方案乙的概率;标注答案$\frac{13}{36}$解析解:由(1)知,$P(A)=\frac{1}{3},P(B)=\frac{3}{4}$,
设“这 $3$ 人中恰有 $2$ 人支持方案一”为事件 $C$,
则 $P(C)=C^2_2(\frac{1}{3})^2(1-\frac{3}{4})+C^1_2\cdot\frac{1}{3}\cdot(1-\frac{1}{3})\cdot\frac{3}{4}=\frac{13}{36}$. -
将该校学生支持方案二的概率估计值记为 $p_0$.假设该校一年级有 $500$ 名男生和 $300$ 名女生,除一年级外其他年级学生支持方案二的概率估计值记为 $p_1$,试比较 $p_0$ 与 $p_1$ 的大小.(结论不需求证明)标注答案$p_0>p_1$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3