为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了 $100$ 天空气中的 $PM 2.5$ 和 $SO_2$ 浓度(单位:$\mu\text{g/m}^3$),得下表: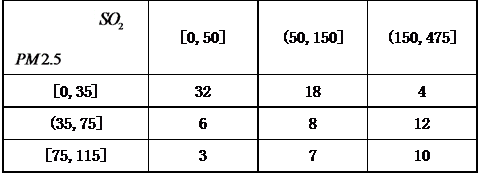 附:$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)},$$
附:$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)},$$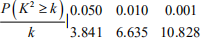
 附:$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)},$$
附:$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)},$$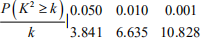
【难度】
【出处】
2020年新高考(Ⅱ)卷
【标注】
-
估计事件“该市一天空气中 $PM2.5$ 浓度不超过 $75$,且 $SO_2$ 浓度不超过 $150$”的概率;标注答案$0.64$解析解:根据抽查数据,该市 $100$ 天的空气中 $PM2.5$ 浓度不超过 $75$,且 $SO_2$ 浓度不超过 $150$ 的天数为 $32+18+6+8=64$.因此,该市一天空气中 $PM2.5$ 浓度不超过 $75$,且 $SO_2$ 浓度不超过 $150$ 的概率的估计值为 $\frac{64}{100}=0.64.$
-
根据所给数据,完成下面的 $2\times2$ 列联表:
 标注答案略解析:根据抽查数据,可得 $2\times2$ 列联表:$$\begin{array}{ccc} & [0,150] & (150,475] \\ [0,75] & 64 & 16 \\ (75,115] & 10 & 10 \end{array}$$
标注答案略解析:根据抽查数据,可得 $2\times2$ 列联表:$$\begin{array}{ccc} & [0,150] & (150,475] \\ [0,75] & 64 & 16 \\ (75,115] & 10 & 10 \end{array}$$ -
根据(2)中的列联表,判断是否有 $99\%$ 把握认为该市一天空气中 $PM2.5$ 浓度与 $SO_2$ 浓度有关?标注答案有把握解析$$K^2=\frac{100\times(64\times10-16\times10)^2}{80\times20\times74\times36}\approx7.484.$$由于 $7.484>6.635$,故由 $99\%$ 的把握认为该市一天空气中 $PM2.5$ 浓度与 $SO_2$ 浓度有关.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3