假设每天从甲地去乙地的旅客人数 $X$ 是服从正态分布 $N\left( {800,{{50}^2}} \right)$ 的随机变量，记一天中从甲地去乙地的旅客人数不超过 $ 900 $ 的概率为 ${P_0}$．
【难度】
【出处】
2013年高考湖北卷（理）
【标注】
-
求 ${P_0}$ 的值；
（参考数据：若 $X \sim N\left( {\mu ,{\sigma ^2}} \right)$，有 $P\left( {\mu - \sigma < X \leqslant \mu + \sigma } \right) = 0.6826 $，$ P\left( {\mu - 2\sigma < X \leqslant \mu + 2\sigma } \right) = 0.9544 $，$P\left( {\mu - 3\sigma < X \leqslant \mu + 3\sigma } \right) = 0.9974$）标注答案$ 0.9772$解析本题由正态分布的公式即可求解．由于随机变量 $X$ 服从正态分布$N\left( {800,{{50}^2}} \right)$，故有\[\mu = 800,\sigma = 50,P\left( {700 < X \leqslant 900} \right) = 0.9544.\]由正态分布的对称性，可得\[\begin{split}{p_0} &= P\left( {X \leqslant 900} \right) \\&= P\left( {X \leqslant 800} \right) + P\left( {800 < X \leqslant 900} \right) \\&= \dfrac{1}{2} + \dfrac{1}{2}P\left( {700 < X \leqslant 900} \right) \\&= 0.9772.\end{split}\] -
某客运公司用 $A$，$B$ 两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次，$A$，$B$ 两种车辆的载客量分别为 $ 36 $ 人和 $ 60 $ 人，从甲地去乙地的营运成本分别为 $ 1600 $ 元/辆和 $ 2400 $ 元/辆．公司拟组建一个不超过 $ 21 $ 辆车的客运车队，并要求 $B$ 型车不多于 $A$ 型车 $ 7 $ 辆．若每天要以不小于 ${p_0}$ 的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备 $A$ 型车、$B$ 型车各多少辆？标注答案应配备 $A$ 型车 $ 5 $ 辆，$B$ 型车 $ 12 $ 辆解析本题考查线性规划在实际问题中的应用，关键是建立线性规划的模型．设 $A$ 型、$B$ 型车辆的数量分别为 $x$，$y$，则相应的营运成本为\[1600x + 2400y.\]依题意，$x$，$y$ 还需满足\[x + y \leqslant 21,y \leqslant x + 7,P\left( {X \leqslant 36x + 60y} \right) \geqslant {p_0}.\]由（1）知，${p_0} = P\left( {X \leqslant 900} \right)$，故 $P\left( {X \leqslant 36x + 60y} \right) \geqslant {p_0}$ 等价于 $36x + 60y \geqslant 900$．
于是问题等价于求满足约束条件\[{\begin{cases}
x + y \leqslant 21, \\
y \leqslant x + 7, \\
36x + 60y \geqslant 900, \\
x,y \geqslant 0,x,y \in {\mathbb{N}}, \\
\end{cases}}\]且使目标函数 $z = 1600x + 2400y$ 达到最小的 $x$，$y$．
作可行域如图所示，可行域的三个顶点坐标分别为 $P\left( {5,12} \right)$，$Q\left( {7,14} \right)$，$R\left( {15,6} \right)$．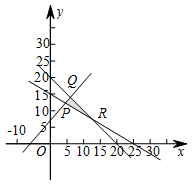
由图可知，当直线 $z = 1600x + 2400y$ 经过可行域的点 $P$ 时，
直线 $z = 1600x + 2400y$ 在 $y$ 轴上截距 $\dfrac{z}{2400}$ 最小，即 $z$ 取得最小值．
故应配备 $A$ 型车 $ 5 $ 辆，$B$ 型车 $ 12 $ 辆．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
