如图,已知椭圆 ${C_1}$ 与 ${C_2}$ 的中心在坐标原点 $O$,长轴均为 $MN$ 且在 $x$ 轴上,短轴长分别为 $2m$,$2n$ $\left( {m > n} \right)$,过原点且不与 $x$ 轴重合的直线 $l$ 与 ${C_1}$,${C_2}$ 的四个交点按纵坐标从大到小依次为 $A$,$B$,$C$,$D$,记 $\lambda = \dfrac{m}{n}$,$\triangle BDM$ 和 $\triangle ABN$ 的面积分别为 ${S_1}$ 和 ${S_2}$.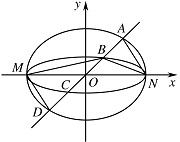

【难度】
【出处】
2013年高考湖北卷(文)
【标注】
-
当直线 $l$ 与 $y$ 轴重合时,若 ${S_1} = \lambda {S_2}$,求 $\lambda $ 的值;标注答案$\lambda =\sqrt 2 +1$解析本题的关键是怎么把面积用 $\lambda$ 来表示,注意 $\lambda$ 与 $m$、$n$ 的关系.依题意,可设 $ C_1$,$C_2 $ 的方程分别为\[\begin{split}{C_1}&:\dfrac {x^2} {a^2} +\dfrac {y^2} {m^2} =1,\\ {C_2}&:\dfrac {x^2} {a^2} +\dfrac {y^2} {n^2} =1, \end{split}\]其中 $0 < n < m < a$,$\lambda = \dfrac m n >1$.
方法一:
如图,若直线 $ l $ 与 $ y $ 轴重合,即直线 $ l $ 的方程为 $ x=0 $,则\[\begin{split} {S_1}&={\dfrac 1 2 }{\left|{BD}\right|} \cdot {\left|{OM}\right|} ={\dfrac 1 2 }a {\left|{BD}\right|}, \\ {S_2}&={\dfrac 1 2 }{\left|{AB}\right|} \cdot {\left|{ON}\right|} ={\dfrac 1 2 }a {\left|{AB}\right|} ,\end{split}\]所以\[\dfrac {S_1} {S_2} =\dfrac {{\left|{BD}\right|}} {{\left|{AB}\right|}} .\]在 ${C_1} $ 和 ${C_2} $ 的方程中分别令 $ x=0 $,可得\[ {y_A}=m,{y_B}=n,{y_D}=-m, \]于是\[\begin{split}\dfrac{{\left|{BD}\right|}}{{\left|{AB}\right|}} &= \dfrac{{\left|{{y_B}-{y_D}}\right|}}{{\left|{{y_A}-{y_B}}\right|}} \\&= \dfrac {m+n} {m-n} \\&= \dfrac {\lambda+1} {\lambda-1} .\end{split}\]若 $ \dfrac {S_1} {S_2} =\lambda $,则 $\dfrac {\lambda +1} {\lambda -1} =\lambda $,化简得\[\lambda^2-2\lambda -1=0 .\]由 $\lambda >1 $,可解得\[\lambda =\sqrt 2 +1.\]故当直线 $ l $ 与 $ y $ 轴重合时,若 ${S_1} =\lambda {S_2} $,则 $\lambda =\sqrt 2 +1$.
方法二:
如图,若直线 $ l $ 与 $ y $ 轴重合,则\[\begin{split}{\left|{BD}\right|}&={\left|{OB}\right|}+{\left|{OD}\right|}=m+n , \\ {\left|{AB}\right|} &= {\left|{OA}\right|}-{\left|{OB}\right|}=m-n; \\ S_1&=\dfrac 1 2 {\left|{BD}\right|} \cdot {\left|{OM}\right|} = \dfrac 1 2 a {\left|{BD}\right|}, \\ S_2&=\dfrac 1 2 {\left|{AB}\right|} \cdot {\left|{ON}\right|} = \dfrac 1 2 a {\left|{AB}\right|}. \end{split}\]所以\[\dfrac {S_1} {S_2} =\dfrac {{\left|{BD}\right|}} {{\left|{AB}\right|}} =\dfrac {m+n} {m-n} = \dfrac {\lambda+1} {\lambda-1} .\]若 $ \dfrac {S_1} {S_2} =\lambda $,则 $\dfrac {\lambda +1} {\lambda -1} =\lambda $,化简得\[\lambda^2-2\lambda -1=0 .\]由 $\lambda >1 $,可解得\[\lambda =\sqrt 2 +1.\]故当直线 $ l $ 与 $ y $ 轴重合时,若 ${S_1} =\lambda {S_2} $,则 $\lambda =\sqrt 2 +1$.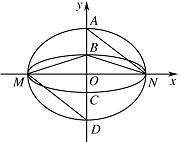
-
当 $\lambda $ 变化时,是否存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda {S_2}$?并说明理由.标注答案当 $1 < \lambda\leqslant 1 + \sqrt 2 $ 时,不存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$;
当 $\lambda > 1 +\sqrt 2 $ 时,存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$解析本题可用弦长公式和点到直线的距离公式表示面积,计算中随时注意化简.方法一:
如图,若存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda {S_2}$,
根据对称性,不妨设直线 $l:y = kx\left( {k > 0} \right)$,点 $M\left( { - a,0} \right)$,$N\left( {a,0} \right)$ 到直线 $l$ 的距离分别为 ${d_1}$,${d_2}$,则\[\begin{split} {d_1} & = \dfrac{| - ak - 0|}{{\sqrt {1 + {k^2}} }} = \dfrac{ak}{{\sqrt{1 + {k^2}} }} ,\\ {d_2} &= \dfrac{|ak - 0|}{{\sqrt {1 + {k^2}} }} = \dfrac{ak}{{\sqrt{1 + {k^2}} }},\end{split} \]所以 ${d_1} = {d_2}$.又\[\begin{split}{S_1} &= \dfrac{1}{2}|BD|{d_1}, \\ {S_2} &= \dfrac{1}{2}|AB|{d_2},\end{split}\]所以\[\dfrac{S_1}{S_2} = \dfrac{|BD|}{|AB|} =\lambda,\]即 $|BD| = \lambda |AB|$.由对称性可知 $|AB| = |CD|$,所以\[\begin{split} |BC| &= |BD| - |AB| = \left( {\lambda - 1} \right)|AB| ,\\ |AD| &= |BD| + |AB| = \left( {\lambda + 1} \right)|AB|,\end{split} \]于是\[\dfrac{|AD|}{|BC|} = \dfrac{{\lambda +
1}}{\lambda - 1} .\quad \cdots \cdots ① \]将 $l$ 的方程分别与 ${C_1}$,${C_2}$ 的方程联立,可求得\[\begin{split} {x_A} &= \dfrac{am}{{\sqrt {{a^2}{k^2} + {m^2}} }}, \\ {x_B} &= \dfrac{an}{{\sqrt {{a^2}{k^2} + {n^2}} }}.\end{split} \]根据对称性可知 ${x_C} = - {x_B}$,${x_D} = - {x_A}$,于是\[\begin{split} \dfrac{|AD|}{|BC|} &= \dfrac{{\sqrt {1 + {k^2}}|{x_A} - {x_D}|}}{{\sqrt {1 + {k^2}} |{x_B} - {x_C}|}} \\ & = \dfrac{{2{x_A}}}{{2{x_B}}}\\ & = \dfrac{m}{n}\sqrt {\dfrac{{{a^2}{k^2} + {n^2}}}{{{a^2}{k^2} + {m^2}}}} . \quad \cdots \cdots ② \end{split} \]从而由 ① 和 ② 式可得\[\sqrt {\dfrac{{{a^2}{k^2} + {n^2}}}{{{a^2}{k^2} +{m^2}}}} = \dfrac{\lambda + 1}{{\lambda \left( {\lambda - 1} \right)}} .\quad \cdots \cdots ③ \]令 $t = \dfrac{\lambda + 1}{{\lambda \left( {\lambda - 1} \right)}}$,则由 $m > n$,可得 $t \ne 1$,于是由 ③ 可解得\[{k^2} =\dfrac{{{n^2}\left( {{\lambda ^2}{t^2} - 1} \right)}}{{{a^2}\left( {1 - {t^2}}\right)}}.\]因为 $k \ne 0$,所以 ${k^2} > 0$.
于是 ③ 式关于 $k$ 有解,当且仅当 $\dfrac{{{n^2}\left({{\lambda ^2}{t^2} - 1} \right)}}{{{a^2}\left( {1 - {t^2}} \right)}} > 0$,等价于\[\left( {{t^2} -1} \right)\left( {{t^2} - \dfrac{1}{\lambda ^2}} \right) < 0.\]由 $\lambda > 1$,可解得 $\dfrac{1}{\lambda} < t < 1$,即\[\dfrac{1}{\lambda} < \dfrac{\lambda + 1}{{\lambda \left( {\lambda - 1} \right)}} < 1.\]由 $\lambda > 1$,解得\[\lambda > 1 +\sqrt 2 .\]所以当 $1 < \lambda\leqslant 1 + \sqrt 2 $ 时,不存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$;
当 $\lambda > 1 +\sqrt 2 $ 时,存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$.
方法二:
如图,若存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$,
根据对称性,不妨设直线 $l:y = kx\left( {k > 0} \right)$,点 $M\left( { - a,0} \right)$,$N\left( {a,0} \right)$ 到直线 $l$ 的距离分别为 ${d_1}$,${d_2}$,因为\[\begin{split}{d_1} &= \dfrac{{|
- ak - 0|}}{{\sqrt {1 + {k^2}} }} = \dfrac{ak}{{\sqrt {1 + {k^2}} }} ,\\ {d_2} &=
\dfrac{|ak - 0|}{{\sqrt {1 + {k^2}} }} = \dfrac{ak}{{\sqrt {1 + {k^2}} }},
\end{split}\]所以 ${d_1} = {d_2}$.又\[\begin{split} {S_1} &=\dfrac{1}{2}|BD|{d_1}, \\ {S_2} &=\dfrac{1}{2}|AB|{d_2},\end{split} \]所以\[\dfrac{S_1}{S_2}= \dfrac{|BD|}{|AB|} = \lambda .\]因为\[\begin{split}\dfrac{|BD|}{|AB|}&= \dfrac{{\sqrt {1 + {k^2}} |{x_B} - {x_D}|}}{{\sqrt {1 + {k^2}} |{x_A} -{x_B}|}} \\&= \dfrac{{{x_A} + {x_B}}}{{{x_A} - {x_B}}} \\&= \lambda ,\end{split}\]所以\[\dfrac{x_A}{x_B}= \dfrac{\lambda + 1}{\lambda - 1}.\]由点 $A\left( {{x_A},k{x_A}} \right)$,$B\left( {{x_B},k{x_B}} \right)$ 分别在 ${C_1}$,${C_2}$ 上,可得\[\begin{split}\dfrac{x_A^2}{a^2}+ \dfrac{{{k^2}x_A^2}}{m^2} &= 1, \\ \dfrac{x_B^2}{a^2}
+ \dfrac{{{k^2}x_B^2}}{n^2} &= 1,
\end{split}\]两式相减可得\[\dfrac{x_A^2 -x_B^2}{a^2} + \dfrac{{{k^2}\left( {x_A^2 - {\lambda ^2}x_B^2}\right)}}{m^2} = 0.\left(*\right)\]依题意得 ${x_A} > {x_B}> 0$,所以 $x_A^2 > x_B^2$.所以由 $ \left(*\right) $ 式可得\[{k^2} =\dfrac{{{m^2}\left( {x_A^2 - x_B^2} \right)}}{{{a^2}\left( {{\lambda ^2}x_B^2 -x_A^2} \right)}}.\]因为 ${k^2} > 0$,所以由 $\dfrac{{{m^2}\left(
{x_A^2 - x_B^2} \right)}}{{{a^2}\left( {{\lambda ^2}x_B^2 - x_A^2} \right)}}
> 0$,可解得\[1 <\dfrac{x_A}{x_B} < \lambda .\]从而 $1 <\dfrac{\lambda + 1}{\lambda - 1} < \lambda $,解得\[\lambda > 1 +\sqrt 2 ,\]所以当 $1 < \lambda\leqslant 1 + \sqrt 2 $ 时,不存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$;
当 $\lambda > 1 +\sqrt 2 $ 时,存在与坐标轴不重合的直线 $l$,使得 ${S_1} = \lambda{S_2}$.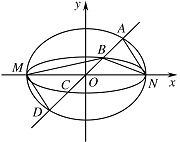
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2