如图,点 $ P\left(0,-1\right) $ 是椭圆 $C_1:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(a > b > 0\right) $ 的一个顶点,$ C_1 $ 的长轴是圆 $C_2:x^2+y^2=4 $ 的直径.$l_1$,$l_2 $ 是过点 $P $ 且互相垂直的两条直线,其中 $l_1 $ 交圆 $ C_2 $ 于 $A$,$B $ 两点,$l_2 $ 交椭圆 $ C_1 $ 于另一点 $ D$.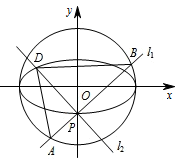

【难度】
【出处】
2013年高考浙江卷(理)
【标注】
-
求椭圆 $C_1 $ 的方程;标注答案$\dfrac{x^2}{4} + {y^2} = 1$解析根据题意确定基本量.由题意得 ${ \begin{cases}
b = 1 \\
a = 2 \\
\end{cases} }$.所以椭圆 $C_1$ 的方程为\[\dfrac{x^2}{4} + {y^2} = 1.\] -
求 $\triangle ABD $ 面积取最大值时直线 $l_1 $ 的方程.标注答案$y = \pm \dfrac{{\sqrt {10} }}{2}x - 1$解析利用弦长公式和点到直线的距离公式表达面积.设 $A\left( {{x_{ 1 }},{y_{ 1 }}} \right)$,$ B\left( {{x_{ 2 }},{y_{ 2 }}} \right) $,$D\left( {{x_0},{y_0}} \right)$.
由题意知直线 ${l_{ 1 }}$ 的斜率存在,不妨设其为 $k$,则直线 ${l_{ 1 }}$ 的方程为\[y = kx - 1.\]又圆 ${C_{ 2 }}:{x^{ 2 }} + {y^{ 2 }} = { 4 }$,故点 $O$ 到直线 ${l_{ 1 }}$ 的距离\[d = \dfrac{1}{{\sqrt {{k^2} + 1} }},\]所以\[ \begin{split}\left| {AB} \right| \overset{\left[a\right]}= 2\sqrt {4 - {d^2}} = 2\sqrt {\dfrac{{4{k^2} + 3}}{{{k^2} + 1}}} .\end{split} \](推导中用到:[a])
又 ${l_1} \perp {l_2}$,故直线 ${l_2}$ 的方程为\[x + ky + k = 0.\]由 ${ \begin{cases}
x + ky + k = 0, \\
\dfrac{x^2}{4} + {y^2} = 1 ,\\
\end{cases} }$ 消去 $y$,整理得\[ \left( {{ 4 } + {k^{ 2 }}} \right){x^{ 2 }} + { 8 }kx = 0,\]故 ${x_0} = - \dfrac{8k}{{4 + {k^2}}}$.所以\[\left| {PD} \right| \overset{\left[b\right]}= \dfrac{{8\sqrt {{k^2} + 1} }}{{4 + {k^2}}}.\](推导中用到:[b])
设 $\triangle ABD$ 的面积为 $S$,则\[ \begin{split}S = \dfrac{1}{2}\left| {AB} \right| \cdot \left| {PD} \right| = \dfrac{{8\sqrt {4{k^2} + 3} }}{{4 + {k^2}}},\end{split} \]所以\[ \begin{split} S & = \dfrac{32}{{\sqrt {4{k^2} + 3} + \dfrac{13}{{\sqrt {4{k^2} + 3} }}}} \\ & \leqslant \dfrac{32}{{2\sqrt {\sqrt {4{k^2} + 3} \cdot \dfrac{13}{{\sqrt {4{k^2} + 3} }}} }} \\ & = \dfrac{{16\sqrt {13} }}{13},\end{split} \]当且仅当 $k = \pm \dfrac{{\sqrt {10} }}{2}$ 时取等号,所以所求直线 ${l_1}$ 的方程为\[y = \pm \dfrac{{\sqrt {10} }}{2}x - 1.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2