如图，在平面直角坐标系 $xOy$ 中，点 $A\left(0,3\right)$，直线 $l:y = 2x - 4$．设圆 $C$ 的半径为 $1$，圆心在 $l$ 上．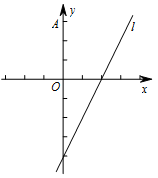
【难度】
【出处】
2013年高考江苏卷
【标注】
-
若圆心 $C$ 也在直线 $y = x - 1$ 上，过点 $A$ 作圆 $C$ 的切线，求切线的方程；标注答案$y = 3$ 或 $ 3x + 4y - 12 = 0$解析按直线的斜率是否存在分类求解，其中用到点到直线的距离等于半径．由题设，圆心 $C$ 是直线 $y = 2x - 4$ 和 $y = x - 1$ 的交点，解得交点为 $C\left( {3,2} \right)$，而半径为 $1$，于是切线的斜率必存在．
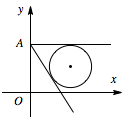设过 $A\left( {0,3} \right)$ 的圆 $C$ 的切线方程为\[y = kx + 3.\]由题意，得\[\dfrac{|3k + 1|}{{\sqrt {{k^2} + 1} }} = 1,\]解得：\[k = 0 或 - \dfrac{3}{4}.\]故所求切线方程为\[y = 3 或 3x + 4y - 12 = 0.\] -
若圆 $C$ 上存在点 $M$，使 $MA = 2MO$，求圆心 $C$ 的横坐标 $a$ 的取值范围．标注答案$\left[ {0,\dfrac{12}{5}} \right]$解析求出动点 $M$ 的轨迹方程是解决本题的关键．因为圆心在直线 $y = 2x - 4$ 上，所以圆 $C$ 的方程为\[{\left( {x - a} \right)^2} + {\left[ {y - 2\left( {a - 2} \right)} \right]^2} = 1.\]设点 $M\left( {x,y} \right)$，因为 $MA = 2MO$，所以 $\sqrt {{x^2} + {{\left( {y - 3} \right)}^2}} = 2\sqrt {{x^2} + {y^2}} $，化简得\[{x^2} + {y^2} + 2y - 3 = 0,\]即\[{x^2} + {\left( {y + 1} \right)^2} = 4,\]所以点 $M$ 在以 $D\left( {0, - 1} \right)$ 为圆心，$ 2 $ 为半径的圆上．
由题意，点 $M\left( {x,y} \right)$ 在圆 $C$ 上，所以圆 $C$ 与圆 $D$ 有公共点，则\[\left| {2 - 1} \right| \leqslant CD \leqslant 2 + 1,\]即\[1 \leqslant \sqrt {{a^2} + {{\left( {2a - 3} \right)}^2}} \leqslant 3.\]整理，得\[ - 8 \leqslant 5{a^2} - 12a \leqslant 0.\]解 $5{a^2} - 12a + 8 \geqslant 0$，得\[a \in {\mathbb{R}};\]解 $5{a^2} - 12a \leqslant 0$，得\[0 \leqslant a \leqslant \dfrac{12}{5}.\]所以点 $C$ 的横坐标 $a$ 的取值范围为 $\left[ {0,\dfrac{12}{5}} \right]$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
