如图,游客从某旅游景区的景点 $A$ 处下山至 $C$ 处有两种路径.一种是从 $A$ 沿直线步行到 $C$,另一种是先从 $A$ 沿索道乘缆车到 $B$,然后从 $B$ 沿直线步行到 $C$.现有甲、乙两位游客从 $A$ 处下山,甲沿 $AC$ 匀速步行,速度为 $50{\mathrm{m {/} min}}$.在甲出发 $2{\mathrm{min}} $ 后,乙从 $A$ 乘缆车到 $B$,在 $B$ 处停留 $1{\mathrm{min}} $ 后,再从 $B$ 匀速步行到 $C$.假设缆车匀速直线运动的速度为 $130{\mathrm{m{/}min}} $,山路 $AC$ 长为 $1260{\mathrm{m}}$,经测量,$\cos A = \dfrac{12}{13},\cos C = \dfrac{3}{5}$.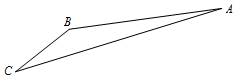

【难度】
【出处】
2013年高考江苏卷
【标注】
-
求索道 $AB$ 的长;标注答案索道 $AB$ 的长为 $1040 {\mathrm{m}}$解析$\triangle ABC$ 中已知两角一边,可以先根据三角形内角和 $180^\circ$ 及和差角公式,求出另一角,再结合正弦定理求出 $AB$.在 $\triangle ABC$ 中,因为 $\cos A = \dfrac{12}{13} , \cos C = \dfrac{3}{5}$,所以根据同角三角函数的基本关系可得\[\sin A = \dfrac{5}{13} , \sin C = \dfrac{4}{5},\]从而\[ \begin{split} \sin B &= \sin \left[ {{\mathrm \pi} - \left( {A + C} \right)} \right] \\ & \overset{\left[a\right]}= \sin \left(A + C\right) \\& \overset{\left[b\right]}= \sin A\cos C + \cos A\sin C \\ & = \dfrac{5}{13} \times \dfrac{3}{5} + \dfrac{12}{13} \times \dfrac{4}{5} \\ & = \dfrac{63}{65}.\end{split} \](推导中用到:[a],[b])
由正弦定理$\dfrac{AB}{\sin C} = \dfrac{AC}{\sin B}$,得\[ \begin{split} AB &= \dfrac{AC}{\sin B} \cdot \sin C \\ & = \dfrac{1260}{{\dfrac{63}{65}}} \times \dfrac{4}{5} \\ & = 1040\left( {\mathrm{m}} \right),\end{split} \]所以索道 $AB$ 的长为 $1040 {\mathrm{m}}$. -
问乙出发多少分钟后,乙在缆车上与甲的距离最短?标注答案$\dfrac{35}{37}\left( {{\mathrm{min}} } \right)$解析假设出发 $t$ 分钟后距离最近,利用余弦定理表达出距离即可.设乙出发 $t{\mathrm{min}} $ 后,甲、乙两游客距离为 $d$,
此时,甲行走了 $\left( {100 + 50t} \right){\mathrm{m}}$,乙距离 $A$ 处 $130t{\mathrm{m}}$,
所以,由余弦定理得\[ \begin{split} {d^2} &= {\left( {100 + 50t} \right)^2} + {\left( {130t} \right)^2} - 2 \times 130t \times \left( {100 + 50t} \right) \times \dfrac{12}{13} \\ & = 200\left( {37{t^2} - 70t + 50} \right).\end{split} \]由于 $0 \leqslant t \leqslant \dfrac{1040}{130}$,即\[0 \leqslant t \leqslant 8,\]故当 $t = \dfrac{35}{37}\left( {{\mathrm{min}} } \right)$ 时,甲、乙两游客距离最短. -
为使两位游客在 $C$ 处互相等待的时间不超过 $3$ 分钟,乙步行的速度应控制在什么范围内?标注答案乙步行的速度应控制在 $\left[ {\dfrac{1250}{43},\dfrac{625}{14}} \right]$(单位:${\mathrm{m{/}min}}$)范围内解析假设乙的步行速度为 $v$,表示出乙到达 $C$ 点需要的时间,同时计算出从乙开始出发时,甲到达 $C$ 点,需要的时间,两个时间差不超过 $3$ 分钟即可.由正弦定理$\dfrac{BC}{\sin A} = \dfrac{AC}{\sin B}$,得\[ \begin{split} BC &= \dfrac{AC}{\sin B} \cdot \sin A \\ & = \dfrac{1260}{{\dfrac{63}{65}}} \times \dfrac{5}{13} \\ & = 500\left( {\mathrm{m}} \right).\end{split} \]乙从 $B$ 出发时,甲已走了\[50 \times \left( {2 + 8 + 1} \right) = 550\left( {\mathrm{m}} \right),\]还需走 $710{\mathrm{m}}$ 才能到达 $C$.设乙步行的速度为 $v{\mathrm{m{/}min}}$,由题意得\[ - 3 \leqslant \dfrac{500}{v} - \dfrac{710}{50} \leqslant 3,\]解此分式不等式得\[\dfrac{1250}{43} \leqslant v \leqslant \dfrac{625}{14},\]所以为使两位游客在 $C$ 处互相等待的时间不超过 $3{\mathrm{min}} $,
乙步行的速度应控制在 $\left[ {\dfrac{1250}{43},\dfrac{625}{14}} \right]$(单位:${\mathrm{m{/}min}}$)范围内.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3