如图，$AB$ 和 $BC$ 分别与圆 $O$ 相切于点 $D$，$C$，$AC$ 经过圆心 $O$，且 $BC = 2OC$．求证：$AC = 2AD$．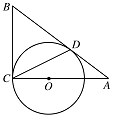
【难度】
【出处】
2013年高考江苏卷
【标注】
-
标注答案略解析连接 $OD$，证明 ${\mathrm{Rt}}\triangle ADO \backsim {\mathrm{Rt}}\triangle ACB$ 即可．如图，连接 $OD$，因为 $AB$ 和 $BC$ 分别与圆 $O$ 相切于点 $D$，$C$，
所以 $\angle ADO = \angle ACB = 90^\circ $，又因为 $\angle A = \angle A$，故 ${\mathrm{Rt}}\triangle ADO \backsim {\mathrm{Rt}}\triangle ACB$，
所以 $\dfrac{BC}{OD} = \dfrac{AC}{AD} $，又 $BC = 2OC = 2OD $，故 $AC = 2AD$．
题目
问题1
答案1
解析1
备注1
