如图，$CD$ 为 $\triangle ABC$ 外接圆的切线，$AB$ 的延长线交直线 $CD$ 于点 $D$，$E$、$F$ 分别为弦 $AB$ 与弦 $AC$ 上的点，且 $BC \cdot AE = DC \cdot AF$，$B,E,F,C$ 四点共圆．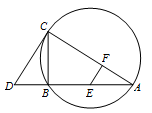
【难度】
【出处】
2013年高考新课标Ⅱ卷（理）
【标注】
-
证明：$CA$ 是 $\triangle ABC$ 外接圆的直径；标注答案略解析本题利用弦切角定理研究相似三角形为证明关键．因为 $CD$ 为 $\triangle ABC$ 外接圆的切线，所以 $\angle DCB = \angle A$．由题设知\[\dfrac{BC}{FA} = \dfrac{DC}{EA},\]故 $\triangle CDB \backsim \triangle AEF$，所以\[\angle DBC = \angle EFA,\]因为 $B,E,F,C$ 四点共圆，所以 $\angle CFE = \angle DBC$，故\[\angle EFA = \angle CFE = 90^\circ,\]所以 $\angle CBA = 90^\circ $．因此 $CA$ 是 $\triangle ABC$ 外接圆的直径．
-
若 $DB = BE = EA$，求过 $B,E,F,C$ 四点的圆的面积与 $\triangle ABC$ 外接圆面积的比值．标注答案$\dfrac{1}{2}$解析本题考查圆幂定理相关知识．如图，连接 $CE$．
因为 $\angle CBE = 90^\circ $，所以过 $B,E,F,C$ 四点的圆的直径为 $CE$，由 $DB = BE$，有 $CE = DC$．又 $\triangle CDB \backsim \triangle ACB$，所以\[B{C^2} = DB \cdot BA = 2D{B^2},\]所以\[C{A^2} = 4D{B^2} + B{C^2} = 6D{B^2},\]而\[C{E^2} = D{C^2} \overset{\left[a\right]}= DB \cdot DA = 3D{B^2}.\]（推导中用到[a]）
故过 $B,E,F,C$ 四点的圆的面积与 $\triangle ABC$ 外接圆面积的比值为 $\dfrac{1}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
