如图，直线 $AB$ 为圆的切线，切点为 $B$，点 $C$ 在圆上，$\angle ABC$ 的角平分线 $BE$ 交圆于点 $E$，$DB$ 垂直 $BE$ 交圆于 $D$．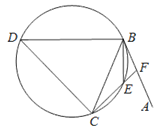
【难度】
【出处】
2013年高考新课标I卷（理）
【标注】
-
证明：$DB = DC$；标注答案略解析本题考查弦切角定理的应用．根据题意证明三角形全等得到．如图，连接 $DE$，交 $BC$ 于点 $G$．
由弦切角定理，得 $\angle ABE = \angle BCE$，
而 $\angle ABE = \angle CBE$，故 $\angle CBE = \angle BCE$，所以 $BE = CE$．
又因为 $DB \perp BE$，所以 $DE$ 为圆的直径，$\angle DCE = 90^\circ $．
所以 $\triangle DBE\cong\triangle DCE$，所以 $DB = DC$． -
设圆的半径为 $1$，$BC = \sqrt 3 $，延长 $CE$ 交 $AB$ 于点 $F$，求 $\triangle BCF$ 外接圆的半径．标注答案$\dfrac{\sqrt 3 }{2}$解析本题考查弦切角定理的应用．由 $(1)$ 知，$\angle CDE = \angle BDE$，$DB = DC$，
故 $DG$ 是 $BC$ 边的中垂线，所以 $BG = \dfrac{\sqrt 3 }{2}$．
如图，设 $DE$ 的中点为 $O$，连接 $BO$，
则 $\angle BOG = 60^\circ $，
从而 $\angle ABE = \angle BCE = \angle CBE = 30^\circ $，所以 $CF \perp BF$，
故 ${ \mathrm {Rt} }\triangle BCF$ 外接圆的半径等于 $ \dfrac12BC=\dfrac{\sqrt 3 }{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
