已知函数 $f\left( x \right) = \left| {2x - 1} \right| + \left| {2x + a} \right|$，$g\left( x \right) = x + 3$．
【难度】
【出处】
2013年高考新课标I卷（理）
【标注】
-
当 $a = - 2$ 时，求不等式 $f\left( x \right) < g\left( x \right)$ 的解集；标注答案$\left\{ {x\left|\right.0 < x < 2 } \right\}$解析本题考查分段函数的图象解决不等式问题．当 $a = - 2$ 时，不等式 $f\left( x \right) < g\left( x \right)$ 化为\[\left| {2x - 1} \right| + \left| {2x - 2} \right| - x - 3 < 0.\]设函数 $y = \left| {2x - 1} \right| + \left| {2x - 2} \right| - x - 3$，则\[y = {\begin{cases}- 5x,&x < \dfrac{1}{2} ,\\
- x - 2,&\dfrac{1}{2} \leqslant x \leqslant 1, \\
3x - 6,&x > 1, \\
\end{cases}}\]其图象如图所示：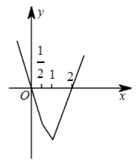
由图象可知，当且仅当 $x \in \left( {0,2} \right)$ 时，$y < 0$，
所以原不等式的解集是 $\left\{ {x\left|\right.0 < x < 2 } \right\}$． -
设 $a > - 1$，且当 $x \in \left[ { - \dfrac{a}{2},\dfrac{1}{2}} \right)$ 时，$f\left( x \right) \leqslant g\left( x \right)$，求 $a$ 的取值范围．标注答案$\left( { - 1,\dfrac{4}{3}} \right]$解析本题考查不等式恒成立的问题．构造新函数，考虑新函数的最大值小于零，或最小值大于零．当 $x \in \left[ { - \dfrac{a}{2},\dfrac{1}{2}} \right)$ 时，\[f\left( x \right) = 1 + a,\]不等式 $f\left( x \right) \leqslant g\left( x \right)$ 化为\[1 + a \leqslant x + 3,\]所以 $x \geqslant a - 2$ 对 $x \in \left[ { - \dfrac{a}{2},\dfrac{1}{2}} \right)$ 恒成立，故\[ - \dfrac{a}{2} \geqslant a - 2,\]即\[a \leqslant \dfrac{4}{3}.\]从而 $a$ 的取值范围是 $\left( { - 1,\dfrac{4}{3}} \right]$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
