已知 $\triangle ABC$ 是边长为 $2$ 的等边三角形，$P$ 为平面 $ABC$ 内一点，则 $\overrightarrow{PA}\cdot \left(\overrightarrow{PB}+\overrightarrow{PC}\right)$ 的最小值 \((\qquad)\)
【难度】
【出处】
2017年高考全国甲卷（理）
【标注】
【答案】
B
【解析】
取 $BC$ 中点，记为 $M$，取 $AM$ 中点，记为 $N$，如图，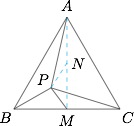
则有\[\begin{split}\overrightarrow{PA}\cdot\left(\overrightarrow{PB}+\overrightarrow{PC}\right)&=\overrightarrow{PA}\cdot2\overrightarrow{PM}\\&\overset{[a]}=2\left(PN^2-\dfrac14AM^2\right)\\&\geqslant2\cdot\left[0-\dfrac14\cdot\left(\sqrt3\right)^2\right]\\&=-\dfrac32.\end{split}\]（推导中用到：[a]）
当且仅当 $P$ 与 $N$ 重合时，取得等号．
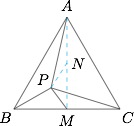则有\[\begin{split}\overrightarrow{PA}\cdot\left(\overrightarrow{PB}+\overrightarrow{PC}\right)&=\overrightarrow{PA}\cdot2\overrightarrow{PM}\\&\overset{[a]}=2\left(PN^2-\dfrac14AM^2\right)\\&\geqslant2\cdot\left[0-\dfrac14\cdot\left(\sqrt3\right)^2\right]\\&=-\dfrac32.\end{split}\]（推导中用到：[a]）当且仅当 $P$ 与 $N$ 重合时，取得等号．
题目
答案
解析
备注
