如图,抛物线 ${C_1}:{x^2} = 4y,{C_2}:{x^2} = - 2py\left( {p > 0} \right)$.点 $M\left( {{x_0},{y_0}} \right)$ 在抛物线 ${C_2}$ 上,过 $ M $ 作 $ {C_1} $ 的切线,切点为 $ A,B $($ M $ 为原点 $ O $ 时,$ A,B $ 重合于 $ O $).当 $ {x_0} = 1 - \sqrt 2 $ 时,切线 $ MA $ 的斜率为 $ - \dfrac{1}{2}$.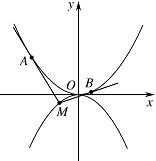

【难度】
【出处】
2013年高考辽宁卷(文)
【标注】
-
求 $ p$ 的值;标注答案$ p = 2$解析利用点 $M$ 即在切线上和又在抛物线上,建立方程组,求出点 $M$ 的纵坐标即可.因为抛物线 ${C_1}:{x^2} = 4y$ 上任意一点 $\left(x,y\right) $ 的切线斜率为\[{y'} = \dfrac{x}{2},\]且切线 $MA $ 的斜率为 $ - \dfrac{1}{2}$,所以 $A $ 点坐标为 $\left( { -1,\dfrac{1}
{4}} \right)$.
故切线 $ MA $ 的方程为\[y = - \dfrac{1}{2}\left( {x + 1} \right) + \dfrac{1}{4}.\]因为点 $M\left( {1 - \sqrt 2 ,{y_0}} \right)$ 在切线 $ MA $ 及抛物线 ${C_2} $ 上,于是\[\begin{split}{y_0} &= - \dfrac{1}{2}\left( {2 - \sqrt 2 } \right) + \dfrac{1}{4} = - \dfrac{3 - 2\sqrt 2 }{4}, \quad \cdots \cdots ① \\ {y_0} &= - \dfrac{{{{\left( {1 - \sqrt 2 } \right)}^2}}}{2p} = - \dfrac{3 - 2\sqrt 2 }{2p}. \quad \cdots \cdots ② \end{split}\]由 ①② 得\[ p = 2 .\] -
当 $ M $ 在 $ {C_2} $ 上运动时,求线段 $ AB $ 中点 $ N $ 的轨迹方程($ A,B $ 重合于 $ O $ 时,中点为 $ O $).标注答案${x^2} = \dfrac{4}{3}y$解析以点 $A,B$ 为参数引入,表示出其中点的横纵坐标,再结合动点是两条切线的交点,且在抛物线上,建立方程组,将参数消掉,得到轨迹方程.设 $N\left( {x,y} \right), A\left( {{x_1},\dfrac{x_1^2}{4}} \right), B\left( {{x_2}\dfrac{x_2^2}{4}} \right), {x_1} \ne {x_2}$,由 $N $ 为线段 $ AB $ 中点知\[x= \dfrac{x_1 + x_2}{2}, \quad \cdots \cdots ③ \\ y = \dfrac{x_1^2 + x_2^2}{8}. \quad \cdots \cdots ④ \]切线 $MA, MB $ 的方程为\[y = \dfrac{x_1}{2}\left( {x - {x_1}} \right) + \dfrac{x_1^2}{4}, \quad \cdots \cdots ⑤ \\ y = \dfrac{x_2}{2}\left( {x - {x_2}} \right) + \dfrac{x_2^2}{4}. \quad \cdots \cdots ⑥ \]由 ⑤⑥ 得 $MA, MB $ 的交点 $M\left( {{x_0},{y_0}} \right)$ 的坐标为\[{x_0} = \dfrac{{{x_1} + {x_2}}}{2},{y_0} = \dfrac{{{x_1}{x_2}}}{4}.\]因为点 $M\left( {{x_0},{y_0}} \right)$ 在 $ {C_2} $ 上,即 $ x_0^2 = - 4{y_0} $,所以\[ {x_1}{x_2} = -\dfrac{x_1^2 + x_2^2}{6} . \quad \cdots \cdots ⑦ \]由 ③④⑦ 得\[{x^2} = \dfrac{4}{3}y,x \ne 0.\]当 ${x_1} = {x_2}$ 时,$ A,B $ 重合于原点 $ O$,$ AB $ 中点 $ N $ 为 $ O$,坐标满足\[{x^2} = \dfrac{4}{3}y.\]因此 $ AB $ 中点 $ N $ 的轨迹方程为\[{x^2} = \dfrac{4}{3}y.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2