如图,$AB$ 为 $ \odot O$ 直径,直线 $CD$ 与 $ \odot O$ 相切于 $E$,$AD$ 垂直 $CD$ 于 $D$,$BC$ 垂直 $CD$ 于 $C$,$EF$ 垂直 $AB$ 于 $F$,连接 $AE,BE$.证明: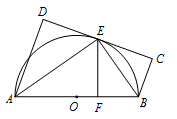

【难度】
【出处】
2013年高考辽宁卷(文)
【标注】
-
$\angle FEB = \angle CEB$;标注答案略解析注意到 $\angle CEB$ 为 $\odot O$ 的弦切角,故只需证明 $\angle FEB=\angle EAB$ 即可.由直线 $CD$ 与 $ \odot O$ 相切,得 $\angle CEB = \angle EAB$.由 $AB$ 为 $ \odot O$ 的直径,得 $AE \perp EB$,从而\[\angle EAB + \angle EBF = \dfrac{\mathrm \pi} {2};\]又 $EF \perp AB$,得\[\angle FEB + \angle EBF = \dfrac{\mathrm \pi} {2}.\]从而 $\angle FEB = \angle EAB$.故\[\angle FEB = \angle CEB.\]
-
$E{F^2} = AD \cdot BC$.标注答案略解析根据射影定理,可知 $EF^2=AF\cdot BF$,因此可以考虑证明 $AD=AF,BF=BC$.由 $BC \perp CE$,$EF \perp AB$,$\angle FEB = \angle CEB$,$BE$ 是公共边,得\[{\mathrm{Rt}}\triangle BCE \cong {\mathrm{Rt}}\triangle BFE,\]所以 $BC = BF$.类似可证 ${\mathrm{Rt}}\triangle ADE \cong {\mathrm{Rt}}\triangle AFE$,得\[AD = AF.\]又在 ${\mathrm{Rt}}\triangle AEB$ 中,$EF \perp AB$,故\[E{F^2} = AF \cdot BF,\]所以\[E{F^2} = AD \cdot BC.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2