如图,已知双曲线 ${C_1}:\dfrac{{{x^2}}}{2} - {y^2} = 1$,曲线 ${C_2}:{\left|{y}\right|} = {\left|{x}\right|} + 1$.$P$ 是平面内一点,若存在过点 $P$ 的直线与 ${C_1}$、${C_2}$ 都有公共点,则称 $P$ 为“${C_1} - {C_2}$ 型点”.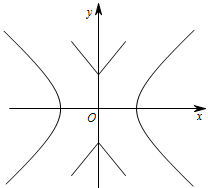

【难度】
【出处】
2013年高考上海卷(理)
【标注】
-
在正确证明 ${C_1}$ 的左焦点是“${C_1} - {C_2}$ 型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);标注答案略解析由 $ {C_1} $ 方程:$ \dfrac{{{x^2}}}{2} - {y^2} = 1 $ 可知\[{a^2} = 2,{b^2} = 1,{c^2} = {a^2} + {b^2} = 3,{F_1}\left( - \sqrt 3 ,0\right).\]显然,由双曲线 ${C_1}$ 的几何图像性质可知,过 ${F_1}$ 的任意直线都与曲线 $ {C_1} $ 相交.
在曲线 ${C_2}$ 图像上取点 $ P\left(0,1\right) $,则直线 $P{F_1}$ 与两曲线 ${C_1}$、$ {C_2} $ 均有交点.
这时直线方程为\[y = \dfrac{{\sqrt 3 }}{3}\left(x + \sqrt 3 \right) \Rightarrow \sqrt 3 y - x - \sqrt 3 = 0.\]所以,$ C_{1} $ 的左焦点是“$ C_{1}-C_{2} $ 型点”.过该焦点的一条直线方程是 $\sqrt 3 y - x - \sqrt 3 = 0$. -
设直线 $y = kx$ 与 ${C_2}$ 有公共点,求证 ${\left|{k}\right|} > 1$,进而证明原点不是“${C_1} - {C_2}$ 型点”;标注答案略解析先证明“若直线 $ y=kx $ 与 ${C_2}$ 有公共点,则 $\left| k \right| >1$”.
双曲线 ${C_1}$ 的渐近线为\[y = \pm \dfrac{b}{a}x = \pm \dfrac{1}{{\sqrt 2 }}x.\]若直线 $ y = kx $ 与双曲线 $ {C_1} $ 有交点,则 $k \in A = \left( - \dfrac{1}{{\sqrt 2 }},\dfrac{1}{{\sqrt 2 }}\right)$.
若直线 $ y = kx $ 与曲线 $ {C_2} $ 有交点,则 $k \in B = \left(-\infty ,-1\right) \cup \left(1,\infty \right)$.
所以,若直线 $ y = kx $ 与 ${C_2}$ 有公共点,则 $\left| k \right| >1 $.
因为 $ A \cap B = \varphi $,所以 直线 $ y = kx $ 与曲线 $ {C_1} $、$ {C_2} $ 不能同时有公共交点.
所以原点不是“$ C_{1}-C_{2} $ 型点”. -
求证:圆 ${x^2} + {y^2} = \dfrac{1}{2}$ 内的点都不是“${C_1} - {C_2}$ 型点”.标注答案略解析设直线 $l$ 过圆 ${x^2} + {y^2} = \dfrac{1}{2}$ 内一点,则斜率不存在时直线 $l$ 与双曲线 ${C_1}$ 无交点.
设直线 $l$ 方程为:$ y = kx + m $,显然当 $ k=0 $ 时,直线 $l$ 与双曲线 ${C_1}$ 不相交.
经计算,圆 ${x^2} + {y^2} = \dfrac{1}{2}$ 内所有点均在曲线 ${C_2} :\left| y \right| = \left| x \right| + 1$ 的延长线所围成的区域内,所以
当 $k = \pm \dfrac{b}{a} = \pm \dfrac{1}{{\sqrt 2 }}$ 时,直线 $l$ 与曲线 ${C_1}$ 不相交.
若直线 $l$ 与曲线 ${C_2}$ 相交,则 ${k^2} > 1 . \quad \cdots \cdots ① $
下面讨论 $k \ne \pm \dfrac{1}{{\sqrt 2 }}$ 时的情况.
圆心到直线 $l$ 的距离\[\dfrac{{ \left|m \right|}}{{\sqrt {{k^2} + 1} }} < \dfrac{1}{{\sqrt 2 }} \Rightarrow 2{m^2} - 1 < {k^2} . \quad \cdots \cdots ② \]假设直线 $l$ 与曲线 ${C_1}$ 相交,联立方程\[\begin{split}{\begin{cases}
\dfrac{{{x^2}}}{2} - {y^2} = 1 \\
y = kx + m \\
\end{cases}} & \Rightarrow {x^2} - 2\left({k^2}{x^2} + 2kmx + {m^2}\right) = 2 \\& \Rightarrow \left(2{k^2} - 1\right){x^2} + 4kmx + 2{m^2} + 2 = 0,k \ne \pm \dfrac{1}{{\sqrt 2 }} \\& \Rightarrow \Delta = {\left(4km\right)^2} - 4\left(2{k^2} - 1\right)\left(2{m^2} + 2\right) \geqslant 0 \\& \Rightarrow 2{k^2} \leqslant 1 + {m^2}. \quad \cdots \cdots ③ \end{split}\]由 $ ①②③ $ 得\[{\begin{cases}2{k^2} > 2 \\
2{k^2} > 4{m^2} - 2 \\
2{k^2} \leqslant 1 + {m^2} \\
\end{cases}} \Rightarrow {\begin{cases}4{m^2} - 2 < 1 + {m^2} \\
2 < 1 + {m^2} \\
\end{cases}} \Rightarrow {\begin{cases}{m^2} < 1 \\
1 < {m^2} \\
\end{cases}} \Rightarrow m \in \varphi \]所以,过圆 ${x^2} + {y^2} = \dfrac{1}{2}$ 内任意一点做任意直线,均不存在与曲线 ${C_1}$ 和 ${C_2}$ 同时相交.即圆 ${x^2} + {y^2} = \dfrac{1}{2}$ 内的点都不是“$ C_{1}-C_{2} $ 型点”.(证毕)
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3