如图,$ \odot O $ 和 $ \odot O' $ 相交于 $ A$,$B $ 两点,过 $ A $ 作两圆的切线分别交两圆于 $ C$,$ D $ 两点,连接 $ DB $ 并延长交 $ \odot O $ 于点 $ E $.证明: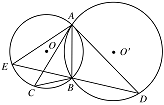

【难度】
【出处】
2012年高考辽宁卷(文)
【标注】
-
$ AC\cdot BD=AD\cdot AB $;标注答案略解析由 $ AC $ 与 $ \odot O' $ 相切于 $ A $,得 $ \angle CAB=\angle ADB $.同理 $ \angle ACB=\angle DAB $,所以 $ \triangle ACB\backsim \triangle DAB$,从而\[ {\dfrac{AC}{AD}}={\dfrac{AB}{BD}}, \]即 $ AC\cdot BD=AD\cdot AB$.
-
$ AC=AE $.标注答案略解析由 $ AD $ 与 $ \odot O $ 相切于 $ A $,得 $ \angle AED=\angle BAD$.又 $ \angle ADE=\angle BDA $,得\[ \triangle EAD\backsim \triangle ABD.\]从而\[ {\dfrac{AE}{AB}}={\dfrac{AD}{BD}},\]即 $ AE\cdot BD=AD\cdot AB$,结合(1)的结论,$ AC=AE $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2