查看数据源：599165ca2bfec200011e1c06
某多面体的三视图如图所示．其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为 $2$，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为  \((\qquad)\)  
A: $10$
B: $12$
C: $14$
D: $16$
【难度】
【出处】
2017年高考全国乙卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的表面积
  • 题型
    >
    立体几何
【答案】
B
【解析】
由三视图可得该几何体的直观图为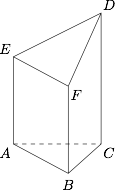： 故所求梯形的面积之和为 $S_{ACDE}+S_{BCDF}=12$．
题目 答案 解析 备注
0.121204s