查看数据源：599165ca2bfec200011e1aaa
如图，已知正四面体 $D-ABC$（所有棱长都相等的三棱锥），$P$，$Q$，$R$ 分别为 $AB$，$BC$，$CA$ 上的点，$AP=PB$，$\dfrac {BQ}{QC}=\dfrac {CR}{RA}=2$，分别记二面角 $D-PR-Q$，$D-PQ-R$，$D-QR-P$ 的平面角为 $\alpha$，$\beta$，$\gamma$，则  \((\qquad)\)  
A: $ \gamma<\alpha<\beta$
B: $\alpha<\gamma<\beta$
C: $\alpha<\beta<\gamma$
D: $\beta<\gamma<\alpha$
【难度】
【出处】
2017年高考浙江卷
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    多面体
    >
    棱锥
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    二面角
  • 题型
    >
    立体几何
【答案】
B
【解析】
由题意，知 $D$ 在底面正三角形的投影为重心 $G$．设 $G$ 到 $PR$、$PQ$、$QR$ 的距离分别为 $d_1$、$d_2$、$d_3$，很明显 $\alpha$，$\beta$，$\gamma$ 均为锐角，且 $\tan \alpha=\dfrac {DG}{d_1}$，$\tan \beta=\dfrac {DG}{d_2}$，$\tan \gamma=\dfrac {DG}{d_3}$，故要比较 $\alpha$，$\beta$，$\gamma$ 的大小关系，只需比较出 $d_1$、$d_2$、$d_3$ 的大小关系即可（大的对应的角小）．由 $AP=PB$，$\dfrac {BQ}{QC}=\dfrac {CR}{RA}=2$ 知，$P$ 为 $AB$ 的中点，$Q$ 为 $BC$ 的一个靠近 $C$ 的三等分点，$R$ 为 $AC$ 的一个靠近 $A$ 的三等分点，取 $P'$ 为 $AB$ 的一个靠近 $B$ 的三等分点，连结 $P'Q$、$P'R$．如图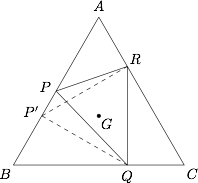 可分析出 $d_1>d_3>d_2$，所以 $\alpha<\gamma<\beta$．
题目 答案 解析 备注
0.203190s