如图25-5由若干个小正方形组成的三角形数阵,第一行有 $1$ 个小正方形,第二行有 $2$ 个小正方形,以此类推,第 $k$ 行有 $k$ 个小正方形,其中 $1\leqslant k\leqslant 11$ 。如图所示,除去最底下的一行,每个小正方形都放置在它下一行的两个小正方形上。第 $11$ 行的小正方形上每个都标注了数字 $0$ 或 $1$,其他小正方形上标注的数字则是它下面两个小正方形上标注的数字之和。请问,最底下的一行中共有多少种标注 $0$ 和 $1$ 的方法使得最顶层小正方形上的数字是 $3$ 的倍数?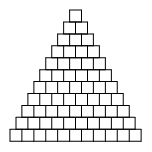

【难度】
【出处】
2007年第25届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
640
【解析】
由底层向顶层将每行标上序号,最底下一行记为第 $0$ 行,最上面一行记为第 $10$ 行。从左到右将第 $10$ 行的每个小正方形依次表示为 ${{x}_{0}}$,${{x}_{1}}$,…,${{x}_{10}}$,其中 ${{x}_{k}}$ 等于 $0$ 或 $1$ 。第 $k$ 行(从下往上数),从左到右每个小正方形上的数依次为 $0$,$1$,…,$10-k$ 。运用归纳法易证第 $k$ 行第 $j$ 个小正方形的数字和(其中 $0\leqslant j\leqslant 10-k$)为
$\displaystyle C_{k}^{0}{{x}_{j+0}}+C_{k}^{1}{{x}_{j+1}}+\ldots+C_{k}^{k}{{x}_{j+k}}=\sum\limits_{i=0}^{k}{{}}C_{k}^{j}{{x}_{j+i}}$,
因此,最顶层(第 $10$ 行)的数字为
$\displaystyle \sum\limits_{i=0}^{10}{{}}C_{10}^{i}{{x}_{i}}$
不难证明,当 $2\leqslant k\leqslant 8$ 时,$C_{10}^{k}$ 是 $3$ 的倍数,因此
$\displaystyle \sum\limits_{i=0}^{10}{{}}C_{10}^{i}{{x}_{i}}={{x}_{0}}+C_{10}^{1}{{x}_{1}}+C_{10}^{9}{{x}_{9}}+{{x}_{10}}$
$={{x}_{0}}+{{x}_{1}}+{{x}_{9}}+{{x}_{10}}\left( \bmod 3 \right)$,
要使最后一个表达式是 $3$ 的倍数,即 ${{x}_{0}}={{x}_{1}}={{x}_{9}}={{x}_{10}}=0$ 或三个数为 $1$,一个数为 $0$,因此要使和为 $3$ 的倍数,${{x}_{0}}$,${{x}_{1}}$,${{x}_{9}}$,${{x}_{10}}$ 有 $5$ 种可能的取值,且 ${{x}_{2}}$ ${{x}_{3}}$,${{x}_{4}}$,…,${{x}_{8}}$ 分别为 $0$ 或 $1$,共有 ${{2}^{7}}$ 中选择方法。因此共有 $5\cdot {{2}^{7}}=640$ 种标注方法使得最顶层的小正方形上的数字是 $3$ 的倍数。
$\displaystyle C_{k}^{0}{{x}_{j+0}}+C_{k}^{1}{{x}_{j+1}}+\ldots+C_{k}^{k}{{x}_{j+k}}=\sum\limits_{i=0}^{k}{{}}C_{k}^{j}{{x}_{j+i}}$,
因此,最顶层(第 $10$ 行)的数字为
$\displaystyle \sum\limits_{i=0}^{10}{{}}C_{10}^{i}{{x}_{i}}$
不难证明,当 $2\leqslant k\leqslant 8$ 时,$C_{10}^{k}$ 是 $3$ 的倍数,因此
$\displaystyle \sum\limits_{i=0}^{10}{{}}C_{10}^{i}{{x}_{i}}={{x}_{0}}+C_{10}^{1}{{x}_{1}}+C_{10}^{9}{{x}_{9}}+{{x}_{10}}$
$={{x}_{0}}+{{x}_{1}}+{{x}_{9}}+{{x}_{10}}\left( \bmod 3 \right)$,
要使最后一个表达式是 $3$ 的倍数,即 ${{x}_{0}}={{x}_{1}}={{x}_{9}}={{x}_{10}}=0$ 或三个数为 $1$,一个数为 $0$,因此要使和为 $3$ 的倍数,${{x}_{0}}$,${{x}_{1}}$,${{x}_{9}}$,${{x}_{10}}$ 有 $5$ 种可能的取值,且 ${{x}_{2}}$ ${{x}_{3}}$,${{x}_{4}}$,…,${{x}_{8}}$ 分别为 $0$ 或 $1$,共有 ${{2}^{7}}$ 中选择方法。因此共有 $5\cdot {{2}^{7}}=640$ 种标注方法使得最顶层的小正方形上的数字是 $3$ 的倍数。
答案
解析
备注