已知等轴双曲线 $C:x^2-y^2=a^2$($a>0$)上一定点 $P(x_0,y_0)$ 及双曲线 $C$ 上两动点 $A,B$ 满足 $(\overrightarrow{OA}-\overrightarrow{OP})\cdot (\overrightarrow{OB}-\overrightarrow{OP})=0$.(其中 $O$ 为坐标原点).
【难度】
【出处】
全国高中数学联赛模拟试题(3)
【标注】
-
证明:$(\overrightarrow{OA}+\overrightarrow{OP})\cdot (\overrightarrow{OB}+\overrightarrow{OP})=0$;标注答案略解析设 $A$ 的坐标为 $(x_1,y_1)$,$B$ 的坐标为 $(x_2,y_2)$,则$$x_1^2-y_1^2=a^2,~~~~~ ① $$$$x_2^2-y_2^2=a^2,~~~~~ ② $$$$x_0^2-y_0^2=a^2,~~~~~ ③ $$③ - ①,得$$(x_0+x_1)(x_0-x_1)=(y_0-y_1)(y_0+y_1).~~~~ ④ $$③ - ②,得$$(x_0+x_2)(x_0-x_2)=(y_0-y_2)(y_0+y_2).~~~~~ ⑤ $$由 $(\overrightarrow{OA}-\overrightarrow{OP})\cdot(\overrightarrow{OB}-\overrightarrow{OP})=0$,得$$(x_1-x_0)(x_2-x_0)+(y_1-y_0)(y_2-y_0)=0.~~~~~ ⑥ $$④ $\times$ ⑤ 并与式 ⑥ 比较,得$$(x_1+x_0)(x_2+x_0)+(y_1+y_0)(y_2+y_0)=0,$$即 $(\overrightarrow{OA}+\overrightarrow{OP})\cdot (\overrightarrow{OB}+\overrightarrow{OP})=0$.
-
求 $|\overrightarrow{AB}|$ 的最小值.标注答案略解析如图所示,分别取 $PA, PB$ 的中点 $M,N$,则$$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OP}), \overrightarrow{ON}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OP}),$$则 $\overrightarrow{OM}\cdot \overrightarrow{ON}=0$,即 $\overrightarrow{OM}\perp \overrightarrow{ON}$.
又由 $(\overrightarrow{OA}-\overrightarrow{OP})\cdot(\overrightarrow{OB}-\overrightarrow{OP})=0$,得 $\overrightarrow{PA}\cdot \overrightarrow{PB}=0$,即 $PA\perp PB$.于是,点 $O, M,P,N$ 都在以 $MN$ 为直径的圆上.从而,$|OP|=|MN|\sin\angle OMP$,则$$|MN|=\frac{|OP|}{\sin\angle OMP}\geqslant |OP|=\sqrt{x_0^2+y_0^2},$$其中等号当且仅当 $\angle OMP=90^{\circ}$ 时成立.
又易知 $|AB|=2|MN|$,所以 $|AB|$ 的最小值是 $2\sqrt{x_0^2+y_0^2}$.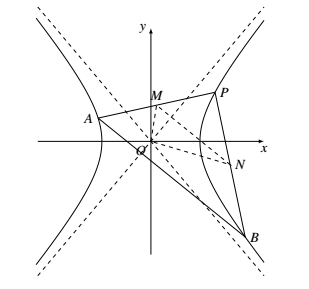
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2