设椭圆 $\frac{x^2}{1+\sin\alpha+\cos\alpha}+\frac{y^2}{\sin\alpha}=1$（$\alpha\in \left(0,\frac{\pi}{2}\right)$）的右焦点为 $F$，经过坐标原点的直线与椭圆交于点 $A,B$．
【难度】
【出处】
全国高中数学联赛模拟试题(6)
【标注】
-
设 $\triangle FAB$ 的面积的最大值为 $S(\alpha)$，试求 $S(\alpha)$ 的表达式（用 $\alpha$ 的代数式表示）；标注答案略解析如图所示，
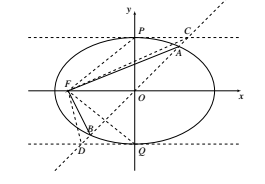设椭圆的上，下顶点分别为 $P,Q$，椭圆在点 $P,Q$ 处的切线分别为 $l_1:y=\sqrt{\sin\alpha}, l_2: y=-\sqrt{\sin\alpha}$，直线 $AB$ 与 $l_1,l_2$ 分别交于点 $C,D$，则 $PC\varparallel FO\varparallel DQ$．于是$$S_{\triangle FPD}=S_{\triangle FPO} +S_{\triangle FQO}=S_{\triangle FCO}+S_{\triangle FDO}=S_{\triangle FCD}\geqslant S_{\triangle FAB}.$$上式等号当且仅当点 $A,C,P$ 重合，点 $B,D,Q$ 重合时取到．从而$$\begin{aligned}
S(\alpha)&=S_{\triangle FPQ}=\frac{1}{2}FO\cdot PQ=\frac{1}{2}\sqrt{(1+\sin\alpha+\cos\alpha)-\sin\alpha}\cdot 2\sqrt{\sin\alpha}\\
&=\sqrt{\sin(1+\cos\alpha)}.\\
\end{aligned}$$ -
当 $\alpha$ 变化时，试求 $S(\alpha)$ 的最大值．标注答案略解析由 $S(\alpha)=\sqrt{\sin\alpha(1+\cos\alpha)}$ 和均值不等式，得$$\begin{aligned}
(S(\alpha))^4&=\sin^2\alpha(1+\cos\alpha)^2=(1-\cos^2\alpha)(1+\cos\alpha)^2=(1-\cos\alpha)(1+\cos\alpha)^3\\
&=\frac{1}{3}(3-3\cos\alpha)(1+\cos\alpha)(1+\cos\alpha)(1+\cos\alpha)\\
&\leqslant \frac{1}{3}\left(\frac{(3-3\cos\alpha)+(1+\cos\alpha)+(1+\cos\alpha)+(1+\cos\alpha)}{4}\right)^4\\
&=\frac{1}{3}\cdot \left(\frac{6}{4}\right)^4=\frac{27}{16}.\\
\end{aligned}$$故$$S(\alpha)\leqslant \sqrt[4]{\frac{27}{16}}=\frac{\sqrt[4]{27}}{2}.$$当 $3-3\cos\alpha=1+\cos\alpha$，即 $\cos\alpha=\frac{1}{2}$，亦即 $\alpha=\frac{\pi}{3}$ 时，$S(\alpha)$ 取到最大值 $\frac{\sqrt[4]{27}}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
