在平面内，过点 $P$ 作直线 $l$ 的垂线所得的垂足称为点 $P$ 在直线 $l$ 上的投影，由区域 $\begin{cases}x-2\leqslant 0,\\ x+y\geqslant 0,\\ x-3y+4\geqslant 0\end{cases}$ 中的点在直线 $x+y-2=0$ 上的投影构成的线段记为 $AB$，则 $|AB|=$ \((\qquad)\)
【难度】
【出处】
2016年高考浙江卷（理）
【标注】
【答案】
C
【解析】
画出可行域，从图形中得到点在直线直线 $x+y-2=0$ 上的投影构成的线段，然后再计算即可．如图 $\triangle PQR$ 为线性区域，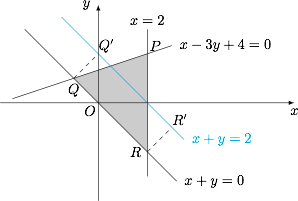
区域内的点在直线 $x+y-2=0$ 上的投影构成了线段 ${R}'{Q}'$，即 $AB$，而 ${R}'{Q}'=RQ$，由\[ \begin{cases}
x-3y+4=0, \\
x+y=0 \\
\end{cases} \]得 $Q\left(-1,1\right)$，由\[\begin{cases}x=2, \\
x+y=0 \\
\end{cases} \]得 $R\left(2,-2\right)$，所以 $\left| AB \right|=\left| QR \right|=\sqrt{{{\left(-1-2\right)}^{2}}+{{\left(1+2\right)}^{2}}}=3\sqrt{2}$．
区域内的点在直线 $x+y-2=0$ 上的投影构成了线段 ${R}'{Q}'$，即 $AB$，而 ${R}'{Q}'=RQ$，由\[ \begin{cases}x-3y+4=0, \\
x+y=0 \\
\end{cases} \]得 $Q\left(-1,1\right)$，由\[\begin{cases}x=2, \\
x+y=0 \\
\end{cases} \]得 $R\left(2,-2\right)$，所以 $\left| AB \right|=\left| QR \right|=\sqrt{{{\left(-1-2\right)}^{2}}+{{\left(1+2\right)}^{2}}}=3\sqrt{2}$．
题目
答案
解析
备注
