如图所示，在 $Rt\triangle ABC$ 中，$\angle C=90^{\circ}, BC=1$．以 $A$ 为圆心，$AC$ 为半径画弧交 $AB$ 于点 $D$，在由弧 $\overrightarrow{CD}$ 与直线段 $BD,BC$ 所围成的区域内作内接正方形 $EFGH$，使得 $E$ 在弧 $\overrightarrow{CD}$ 上，$F$ 在 $BD$ 上，$G$ 和 $H$ 在 $BC$ 上．试问：当 $AC$ 的长为何值时，正方形 $EFGH$ 的面积最大？证明你的结论．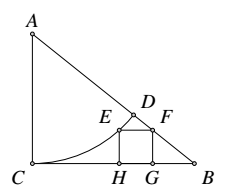
【难度】
【出处】
全国高中数学联赛模拟试题(11)
【标注】
【答案】
略
【解析】
如图所示，设 $AC=x,EF=y$．延长 $FE$ 与 $AC$ 交于 $P$，则 $FP\varparallel BC$，故 $\frac{FP}{AP}=\frac{BC}{AC}$．即$$\frac{FP}{x-y}=\frac{1}{x}\Rightarrow FP=\frac{x-y}{x}.$$在 $Rt\triangle AEP$ 中，$AE=x, AP=x-y, EP=PF-EF=\frac{x-y}{x}-y$，由勾股定理，得$$\left(\frac{x-y}{x}-y\right)^2+(x-y)^2=x^2,~~~~~~~ ① $$即$$(x-y)\left(\frac{x-y}{x^2}-\frac{2y}{x}-2y\right)=0.$$由 $x>y$，知式 ① 成立的充要条件是$$\frac{x-y}{x^2}-\frac{2y}{x}-2y=0.$$
从而$$y=\frac{x}{2x^2+2x+1}=\frac{1}{2x+\frac{1}{x}+2}\leqslant \frac{1}{2\sqrt{2x\cdot \frac{1}{x}}+2}=\frac{1}{2\sqrt{2}+2}.$$等号当且仅当 $2x=\frac{1}{x}$，即 $x=\frac{\sqrt{2}}{2}$ 时取到．
因此，正方形 $EFGH$ 的面积 $y^2$ 当且仅当 $AC=x=\frac{\sqrt{2}}{2}$ 时取得最大值 $\left(\frac{1}{2\sqrt{2}+2}\right)^2=\frac{3-2\sqrt{2}}{4}$
从而$$y=\frac{x}{2x^2+2x+1}=\frac{1}{2x+\frac{1}{x}+2}\leqslant \frac{1}{2\sqrt{2x\cdot \frac{1}{x}}+2}=\frac{1}{2\sqrt{2}+2}.$$等号当且仅当 $2x=\frac{1}{x}$，即 $x=\frac{\sqrt{2}}{2}$ 时取到．因此，正方形 $EFGH$ 的面积 $y^2$ 当且仅当 $AC=x=\frac{\sqrt{2}}{2}$ 时取得最大值 $\left(\frac{1}{2\sqrt{2}+2}\right)^2=\frac{3-2\sqrt{2}}{4}$
答案
解析
备注
