若变量 $x,y$ 满足 $\begin{cases}x+y\leqslant 2,\\ 2x-3y\leqslant 9,\\ x\geqslant 0,\end{cases}$ 则 $x^{2}+y^{2}$ 的最大值是 \((\qquad)\)
【难度】
【出处】
2016年高考山东卷（文）
【标注】
【答案】
C
【解析】
本题考查了非线性规划问题，解决此题的关键之处是知道 $x^2+y^2$ 所表示的几何意义．$x^{2}+y^{2}$ 的几何意义是点 $\left(x,y\right)$ 到原点的距离的平方，要求其最大值，需求可行域中的点到原点的距离的最大值．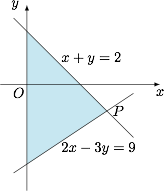
由图可知，$O$ 到 $P$ 处的距离最大，即 $x^{2}+y^{2}$ 的最大值为 $|OP|^{2}=10$．
由图可知，$O$ 到 $P$ 处的距离最大，即 $x^{2}+y^{2}$ 的最大值为 $|OP|^{2}=10$．
题目
答案
解析
备注
