已知过点 $A(1,1)$ 且斜率为 $k$($k<0$)的直线与 $x,y$ 轴分别交于 $P,Q$,过 $P,Q$ 作直线 $2x+y=0$ 的垂线,垂足分别为 $R,S$,求四边形 $PRSQ$ 的面积的最小值.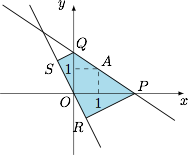

【难度】
【出处】
无
【标注】
【答案】
$\dfrac{18}5$
【解析】
设直线方程为 $\dfrac xa+\dfrac yb=1$($a,b>0$),则 $\dfrac 1a+\dfrac 1b=1$,于是四边形 $PRSQ$ 面积为\[\begin{split}S_{\triangle{OSQ}}+S_{\triangle{OPQ}}+S_{\triangle{OPR}}&=\dfrac{|OQ|^2}{5}+\dfrac 12 |OP|\cdot |OQ|+\dfrac{|OP|^2}{5}\\ &=\dfrac{a^2+b^2}{5}+\dfrac{ab}{2}\\& \geqslant \left(\dfrac 25+\dfrac 12 \right)ab\\ &\geqslant \dfrac{9}{10}\cdot \left(\dfrac{2}{\dfrac 1a+\dfrac 1b}\right)^2=\dfrac{18}{5}.\end{split}\]因此四边形 $PRSQ$ 的面积的最小值为 $\dfrac{18}{5}$,此时 $k=-1$.
答案
解析
备注