查看数据源：599165c92bfec200011e17a7
已知双曲线 $\dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{{{b}^{2}}} = 1$（$b>0$），以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于 $A$，$B$，$C$，$D$ 四点，四边形 $ABCD$ 的面积为 $2b$，则双曲线的方程为 \((\qquad)\)
A: $\dfrac{x^2}{4}-\dfrac{3y^2}{4} = 1$
B: $\dfrac{x^2}{4}-\dfrac{4y^2}{3} = 1$
C: $\dfrac{x^2}{4}-\dfrac{y^2}{4} = 1$
D: $\dfrac{x^2}{4}-\dfrac{y^2}{12} = 1$
【难度】
【出处】
2016年高考天津卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    双曲线
    >
    双曲线的几何量
    >
    双曲线的基本量
  • 题型
    >
    解析几何
【答案】
D
【解析】
由题意，分析出四边形 $ABCD$ 为矩形，且对角线所在直线方程是 $ y=\pm \dfrac b2x $ 是解题的关键．如图，设 $AD$ 与 $x$ 轴交于点 $E$．由题意可得，四边形 $ABCD$ 为矩形．因为 $\tan \angle AOE=\dfrac b2$，$OA=a$，所以 $OE=\dfrac {2}{\sqrt {2^2+b^2}}$，$AE=\dfrac {b}{\sqrt {2^2+b^2}}$，所以四边形 $ABCD$ 的面积为\[\dfrac 12 \times \dfrac {b}{\sqrt {2^2+b^2}} \times\dfrac {2}{\sqrt {2^2+b^2}} \times 8=2b,\]解得 $b^2=12$，所以双曲线的方程为 $\dfrac{x^2}{4}-\dfrac{y^2}{12} = 1$．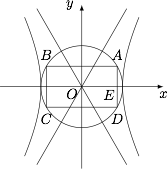
题目 答案 解析 备注
0.206024s