求出所有实数 $x$，使得 $\dfrac{x^2+4x-1}{7x^2-6x-5}$ 与 $\dfrac{1-x}{1+x}$ 同时为整数．
【难度】
【出处】
2014年北京大学全国优秀中学生体验营数学试卷
【标注】
【答案】
$-\dfrac 34,-\dfrac 12,-\dfrac 13,1$
【解析】
显然 $\dfrac{x^2+4x-1}{7x^2-6x-5}\neq 0$，于是\[\left|x^2+4x-1\right|\geqslant\left|7x^2-6x-5\right|,\]解得\[-\dfrac 34\leqslant x\leqslant -\dfrac 13\lor 1\leqslant x\leqslant 2.\]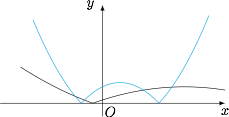
考虑到 $\dfrac{1-x}{1+x}$ 为整数，于是 $x=\dfrac 2k-1$，其中 $k\in\mathbb Z$．于是 $x$ 的所有可能的值为\[1,0,-\dfrac 13,-\dfrac 12,-\dfrac 35,-\dfrac 23,-\dfrac 57,-\dfrac 34,\]逐一验证即得．
考虑到 $\dfrac{1-x}{1+x}$ 为整数，于是 $x=\dfrac 2k-1$，其中 $k\in\mathbb Z$．于是 $x$ 的所有可能的值为\[1,0,-\dfrac 13,-\dfrac 12,-\dfrac 35,-\dfrac 23,-\dfrac 57,-\dfrac 34,\]逐一验证即得．
答案
解析
备注
