如图,在三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,$A{A_1} \perp $ 底面 $ABC$,$BC \perp AC$,$BC = AC = 2$,$A{A_1} = 3$,$D$ 为棱 $AC$ 的中点.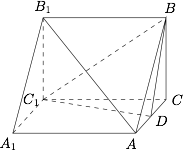

【难度】
【出处】
2013年卓越大学联盟自主选拔录取学科基础测试数学试题
【标注】
-
证明 $A{B_1}\parallel $ 平面 $BD{C_1}$;标注答案略解析连接 ${B_1}C$,交 $B{C_1}$ 于点 $E$,则 $E$ 为 ${B_1}C$ 中点.连接 $DE$.由于 $D$ 为棱 $AC$ 的中点,所以在 $\triangle AC{B_1}$ 中,$A{B_1}\parallel DE$,又因为 $DE \subset $ 平面 $BD{C_1}$,而且 $A{B_1} \not\subset $ 平面 $BD{C_1}$,所以 $A{B_1}\parallel $ 平面 $BD{C_1}$.

-
求直线 $A{B_1}$ 与平面 $BC{C_1}{B_1}$ 所成角的正切值.标注答案$\dfrac{{2\sqrt {13} }}{{13}}$解析因为 $A{A_1} \perp $ 底面 $ABC$,$C{C_1}\parallel A{A_1}$,所以 $C{C_1} \perp $ 底面 $ABC$,故 $C{C_1} \perp AC$.又因 $BC \perp AC$,于是 $AC \perp $ 平面 $BC{C_1}{B_1}$,所以 $\angle AB{ _1}C$ 是直线 $A{B_1}$ 与平面 $BC{C_1}{B_1}$ 所成的角.
在 ${\mathrm {Rt}}\triangle AC{B_1}$ 中,$$AC = 2,B{ _1}C = \sqrt {B{C^2} + BB_1^2} = \sqrt {13}. $$于是$$\tan \angle A{B_1}C = \dfrac{{AC}}{{{B_1}C}} = \dfrac{2}{{\sqrt {13} }} = \dfrac{{2\sqrt {13} }}{{13}}.$$所以,直线 $A{B_1}$ 与平面 $BC{C_1}{B_1}$ 所成角的正切值为 $\dfrac{{2\sqrt {13} }}{{13}}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2