查看数据源：590fcdab857b420007d3e59f
某乒乓球培训班共有 $n$ 位学员，在班内双打训练赛期间，每两名学员都作为搭档恰好参加过一场双打比赛．试确定 $n$ 的所有可能值并分别给出对应的一种安排比赛的方案．
【难度】
【出处】
2012年清华大学（高水平大学）自主选拔学业能力测试
【标注】
  • 数学竞赛
    >
    简单组合
    >
    简单组合
  • 题型
    >
    组合数学
    >
    组合构造
  • 方法
    >
    论述方式
    >
    数学归纳法
  • 方法
    >
    思考方式
    >
    递推与递归
【答案】
$n = 4k$ 或 $n = 4k + 1$，$k \in \mathbb N^*$
【解析】
$n$ 的所有可能值为 $n = 4k$ 或 $n = 4k + 1$，$k \in \mathbb N^*$．
双打比赛总共进行的场次为 $\dfrac{1}{2}\mathrm{C}_n^2 = \dfrac{{n\left( {n - 1} \right)}}{4}$，因此 $n = 4k$ 或 $n = 4k + 1$，$k \in \mathbb N^*$．
下面证明任意 $n = 4k$ 或 $n = 4k + 1$（$k \in \mathbb N^*$）时，都可以构造出满足要求的比赛方案．
将 $n$ 个人看作平面上的 $n$ 个不同的点，则每场双打比赛可以看成是两条无公共端点的线段 ${P_1}{P_2}$、${P_3}{P_4}$ 形成的线段组 ${P_1}{P_2} - {P_3}{P_4}$，题意即 $\dfrac{{n\left( {n - 1} \right)}}{2}$ 条线段可以组成 $\dfrac{{n\left( {n - 1} \right)}}{4}$ 个无公共端点的线段组．
当 $k = 1$ 时，即 $n = 4$ 或 $n = 5$ 时，可以如图构造出符合题意的线段组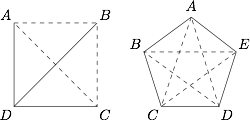：$n = 4$ 时，将 $6$ 条线段分为 $3$ 个线段组：$$AB - CD , AD - BC , BD - AC;$$$n = 5$ 时，将 $10$ 条线段分为 $5$ 个线段组：$$AB - CE , BC - AD , CD - BE , DE - AC , AE - BD.$$假设当 $n = 4k$ 或 $n = 4k + 1$ 可以构造出符合题意的线段组．
情形一 $n = 4k + 4$ 时，设端点为$$A, B, C, D, {P_1}, {Q_1}, {P_2}, {Q_2}, \cdots , {P_{2k}}, {Q_{2k}},$$于是
$(a)$ 根据 $n = 4$ 的情形，可以安排 $A, B, C, D$ 之间的比赛；
$(b)$ 根据 $n = 4k$ 的情形，可以安排 ${P_1}, {Q_1}, {P_2}, {Q_2}, \cdots , {P_{2k}}, {Q_{2k}}$ 之间的比赛；
$(c)$ 安排组间比赛$${P_i}A - {Q_i}B , {P_i}C - {Q_i}D , {P_i}B - {Q_i}A , {P_i}D - {Q_i}C,$$其中 $i = 1, 2, \cdots , 2k$，此时从每个点出发的线段都在线段组中出现过，且所有线段组都无公共端点．
这就证明了当 $n = 4k + 4$ 时可以构造出符合题意的线段组．
情形二 $n = 4k + 5$ 时，设端点为$$A, B, C, D, E, {P_1}, {Q_1}, {P_2}, {Q_2}, \cdots , {P_{2k}}, {Q_{2k}}$$于是
$(a)$ 根据 $n = 5$ 的情形，可以安排 $A, B, C, D, E$ 之间的比赛；
$(b)$ 根据 $n = 4k + 1$ 的情形，可以安排 $E, {P_1}, {Q_1}, {P_2}, {Q_2}, \cdots , {P_{2k}}, {Q_{2k}}$ 之间的比赛；
$(c)$ 安排组间比赛$${P_i}A - {Q_i}B , {P_i}C - {Q_i}D , {P_i}B - {Q_i}A , {P_i}D - {Q_i}C,$$其中 $i = 1, 2, \cdots , 2k$，此时从每个点出发的线段都在线段组中出现过，且所有线段组都无公共端点．
这就证明了当 $n = 4k + 5$ 时可以构造出符合题意的线段组．
综合两种情形，由归纳法原理，命题得证．
答案 解析 备注
0.108218s