如图所示,四棱锥 $P-ABCD$ 的底面为矩形,各棱及底边 $BC,DA$ 的长均为 $a$,$AB,CD$ 的长为 $\sqrt 2a$,过底面对角线 $AC$ 作与 $PB$ 平行的平面交 $PD$ 于 $E$.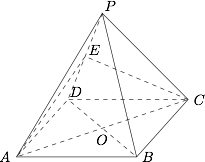

【难度】
【出处】
2012年清华大学暑期学校学业水平测试试题
【标注】
-
求二面角 $E-AC-D$ 的大小;标注答案$\arctan\dfrac{\sqrt 6}4$解析连接 $OE$ 知,$PB\parallel OE$,所以 $E$ 为 $PD$ 的中点.
又因为 $PA=PC=PB=PD$,所以 $PO\perp BD$ 且 $PO\perp AC$,从而有 $PO\perp \text{平面} ABCD$.
取 $OD$ 的中点 $H$,连结 $EH$,在平面 $ABCD$ 上过 $H$ 作 $HF\perp AC$ 于 $F$,连结 $EF$,如图. 容易知道 $\angle EFH$ 即为二面角 $E-AC-D$ 的平面角,$\angle EOD$ 即为 $EO$ 与底面 $ABCD$ 所成的角,容易计算得$$HF=\dfrac {\sqrt 6}6a,EH=\dfrac 12PO=\dfrac a4,OH=\dfrac {\sqrt 3a}4,$$从而有$$\tan\angle EFH=\dfrac {EH}{HF}=\dfrac {\sqrt 6}4,\tan\angle EOD=\dfrac {EH}{OH}=\dfrac {\sqrt 3}3,$$从而有二面角 $E-AC-D$ 的大小为 $\arctan\dfrac{\sqrt 6}4$;
容易知道 $\angle EFH$ 即为二面角 $E-AC-D$ 的平面角,$\angle EOD$ 即为 $EO$ 与底面 $ABCD$ 所成的角,容易计算得$$HF=\dfrac {\sqrt 6}6a,EH=\dfrac 12PO=\dfrac a4,OH=\dfrac {\sqrt 3a}4,$$从而有$$\tan\angle EFH=\dfrac {EH}{HF}=\dfrac {\sqrt 6}4,\tan\angle EOD=\dfrac {EH}{OH}=\dfrac {\sqrt 3}3,$$从而有二面角 $E-AC-D$ 的大小为 $\arctan\dfrac{\sqrt 6}4$; -
记 $AC$ 与 $BD$ 的交点为 $O$,求 $EO$ 与底面 $ABCD$ 所成角的大小;标注答案$\dfrac {\pi}6$解析由 $(1)$ 知 $EO$ 与底面 $ABCD$ 所成角为 $\angle EOD=\dfrac {\pi}6$;
-
求 $DO$ 与平面 $EAC$ 所成角的大小.标注答案$\arcsin{\dfrac {2\sqrt{66}}{33}}$解析由等体积法可以计算出点 $D$ 到平面 $EAC$ 的距离 $d=\dfrac {\sqrt 2}{\sqrt{11}}$(注意,$EH\perp AC$),从而有$$\sin\theta=\dfrac d{OD}=\dfrac {2\sqrt{66}}{33},$$即所求角大小为 $\arcsin{\dfrac {2\sqrt{66}}{33}}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3