正六棱锥的高等于 $h$，相邻侧面的二面角等于 $2\arcsin \dfrac{1}{2}\left( {3\sqrt 2- \sqrt 6 } \right)$，求该棱锥的体积．
【难度】
【出处】
2000年复旦大学保送生招生测试
【标注】
【答案】
$\dfrac{{3 - \sqrt 3 }}{4}{h^3}$
【解析】
如图．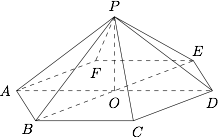
设底面边长为 $a$，则侧棱长为 $\sqrt {{a^2} + {h^2}} $．于是 $\triangle ABP$ 中，$BP$ 边上的高为$$\dfrac{{2{S_{\triangle PAB}}}}{{BP}} = \dfrac{{a\sqrt {\dfrac{3}{4}{a^2} + {h^2}} }}{{\sqrt {{a^2} + {h^2}} }}.$$因此$$\dfrac{1}{2}AC \cdot \dfrac{{\sqrt {{a^2} + {h^2}} }}{{a\sqrt {\dfrac{3}{4}{a^2} + {h^2}} }} = \dfrac{{3\sqrt 2- \sqrt 6 }}{2},$$又 $AC = \sqrt 3 a$，解得 ${a^2} = \dfrac{{\sqrt 3- 1}}{2}{h^2}$．所以$$V = \dfrac{1}{3} \cdot \dfrac{{\sqrt 3 }}{4}{a^2} \cdot 6 \cdot h = \dfrac{{3 - \sqrt 3 }}{4}{h^3}.$$
设底面边长为 $a$，则侧棱长为 $\sqrt {{a^2} + {h^2}} $．于是 $\triangle ABP$ 中，$BP$ 边上的高为$$\dfrac{{2{S_{\triangle PAB}}}}{{BP}} = \dfrac{{a\sqrt {\dfrac{3}{4}{a^2} + {h^2}} }}{{\sqrt {{a^2} + {h^2}} }}.$$因此$$\dfrac{1}{2}AC \cdot \dfrac{{\sqrt {{a^2} + {h^2}} }}{{a\sqrt {\dfrac{3}{4}{a^2} + {h^2}} }} = \dfrac{{3\sqrt 2- \sqrt 6 }}{2},$$又 $AC = \sqrt 3 a$，解得 ${a^2} = \dfrac{{\sqrt 3- 1}}{2}{h^2}$．所以$$V = \dfrac{1}{3} \cdot \dfrac{{\sqrt 3 }}{4}{a^2} \cdot 6 \cdot h = \dfrac{{3 - \sqrt 3 }}{4}{h^3}.$$
答案
解析
备注
