题目 已知棱柱 $ABC - {A_1}{B_1}{C_1}$ 的底面是等腰三角形，$AB = AC$，上底面的顶点 ${A_1}$ 在下底面的射影是 $\triangle ABC$ 的外接圆圆心，设 $BC = a$，$\angle {A_1}AB = \dfrac{{{\pi }}}{3}$，棱柱的侧面积为 $2\sqrt 3 {a^2}$． 问题1 证明：侧面 ${A_1}AB{B_1}$ 和 ${A_1}AC{C_1}$ 都是菱形，${B_1}BC{C_1}$ 是矩形； 答案1 略 解析1 设 ${A_1}$ 在底面 $ABC$ 上的射影为 $O$，则 $O$ 是 $\triangle ABC$ 的外心．所以 $ {A_1}A = {A_1}B$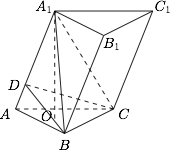．<img src="/static/images/c5850157f25ddaa59f057da88c72229f.png" class="img-responsive" />由 $\angle {A_1}AB = \dfrac{{{\pi }}}{3}$ 知 $ \triangle {A_1}AB $ 是等边三角形．所以 $ A{A_1} = {A_1}B $，所以 $ {A_1}AB{B_1} $ 是菱形．<br/>由对称性知，侧面 $ {A_1}AC{C_1} $ 也是菱形．<br/>由于 $ \triangle ABC $ 中，$ AB = AC $，$ O $ 是其外心，故有 $ AO \perp BC $，即 $ {A_1}A $ 的射影垂直于 $ BC $．<br/>由三垂线定理，$ {A_1}A\perp BC $，故 $ B{B_1} \perp BC $，所以侧面 $ {B_1}BC{C_1}$ 是矩形． 备注1 问题2 求棱柱的侧面所成的三个两面角的大小； 答案2 $\dfrac{{{\pi }}}{3}$ 解析2 设 $A{A_1} = AB = AC = x$，则$$2 \cdot \dfrac{{\sqrt 3 }}{2}{x^2} + ax = 2\sqrt 3 {a^2},$$解得 $ x = \dfrac{2}{{\sqrt 3 }}a$．<br/>过 $B$ 作 $A{A_1}$ 的垂线、垂足为 $D$，则 $\angle BDC$ 为侧面 ${A_1}AB{B_1}$ 与侧面 ${A_1}AC{C_1}$ 的二面角的平面角．<br/>而$$BD = CD = \dfrac{2}{{\sqrt 3 }}a \cdot \sin 60^\circ = a = BC,$$故 $\angle BDC = \dfrac{{{\pi }}}{3}$．又 $DB \perp B{B_1}$，$CB \perp B{B_1}$，故 $\angle DBC$ 是侧面 ${A_1}AB{B_1}$ 与侧面 ${B_1}BC{C_1}$ 的二面角的平面角，大小为 $\dfrac{{{\pi }}}{3}$．<br/>同理，$\angle BCD$ 是侧面 ${A_1}AC{C_1}$ 与侧面 ${B_1}BC{C_1}$ 的二面角的平面角，大小也为 $\dfrac{{{\pi }}}{3}$． 备注2 问题3 求棱柱的体积． 答案3 $ \dfrac{1}{2}{a^3}$ 解析3 因为 ${S_{\triangle BCD}} = \dfrac{{\sqrt 3 }}{4}{a^2}$，而 $B{B_1} = x = \dfrac{{2\sqrt 3 a}}{3}$．所以$${V_{ABC - {A_1}{B_1}{C_1}}} = {S_{\triangle BCD}} \cdot B{B_1} = \dfrac{1}{2}{a^3}.$$ 备注3