设 $A,B$ 为 $y = 1 - {x^2}$ 上在 $y$ 轴两侧的点，求过 $A,B$ 的切线与 $x$ 轴围成面积的最小值．
【难度】
【出处】
2010年北京大学等三校联考自主招生保送生测试
【标注】
【答案】
$\dfrac{{8\sqrt 3 }}{9}$
【解析】
如图．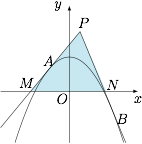
设过 $A,B$ 的切线交于点 $P$，与 $x$ 轴分别交于点 $M,N$．设 $A\left( {x_1},{y_1} \right)$，$B\left( {x_2}, {y_2} \right)$，$P\left( {x_0},{y_0} \right)$，则$${y_1} = 1 - {x_1}^2,\quad {y_2} = 1 - {x_2}^2.$$直线 $AB$：$\dfrac{{y + {y_0}}}{2} = 1 - {x_0}x$，即$$y = - 2{x_0}x + 2 - {y_0}.$$直线 $PA$：$y = - 2{x_1}x + 2 - {y_1}$，直线 $PB$：$y = - 2{x_2}x + 2 - {y_2}$．于是 $M$、$N$ 的横坐标分别为 $\dfrac{{2 - {y_1}}}{{2{x_1}}}$ 和 $\dfrac{{2 - {y_2}}}{{2{x_2}}}$．因此所围成的面积\[\begin{split}S &= \frac{1}{2} \cdot \left| {\frac{{2 - {y_2}}}{{2{x_2}}} - \frac{{2 - {y_1}}}{{2{x_1}}}} \right| \cdot {y_0} \\&= \frac{1}{2}\left| {\frac{{1 + {x_2}^2}}{{2{x_2}}} - \frac{{1 + {x_1}^2}}{{2{x_1}}}} \right| \cdot {y_0} \\&= \left| {\frac{{\left( {{x_1} - {x_2}} \right)\left( {1 - {x_1}{x_2}} \right)}}{{{x_1}{x_2}}}} \right| \cdot \frac{{{y_0}}}{4}.\end{split}\]将直线 $AB$ 与抛物线联立，有$$- 2{x_0}x + 2 - {y_0} = 1 - {x^2},$$即 ${x^2} - 2{x_0}x + 1 - {y_0} = 0$．所以$${x_1}{x_2} = 1-{y_0}, {x_1} + {x_2} = 2{x_0}.$$进而$$\left| {{x_1} - {x_2}} \right| = 2\sqrt {{x_0}^2 + {y_0} - 1} .$$于是$$S = \left| {\frac{{2\sqrt {{x_0}^2 + {y_0} - 1} \cdot {y_0}}}{{1 - {y_0}}}} \right| \cdot \frac{{{y_0}}}{4} = \frac{{{y_0}^2}}{2} \cdot \left| {\frac{{\sqrt {{x_0}^2 + {y_0} - 1} }}{{1 - {y_0}}}} \right|$$因为 ${x_1}, {x_2}$ 异号，于是 ${x_1}{x_2} < 0$，${y_0} - 1 > 0$，于是$$S = \frac{{{y_0}^2}}{{2\left( {{y_0} - 1} \right)}} \cdot \sqrt {{x_0}^2 + \left( {{y_0} - 1} \right)} \geqslant \frac{{{y_0}^2}}{{2\sqrt {{y_0} - 1} }},$$当且仅当 ${x_0} = 0$ 时取等号．
设 $\sqrt {{y_0} - 1} = t$，$t > 0$，则 $S \geqslant \dfrac{{{{\left( {{t^2} + 1} \right)}^2}}}{{2t}}$ 令 $f\left( t \right) = \dfrac{{{{\left( {{t^2} + 1} \right)}^2}}}{t}$，则$$f'\left( t \right) = \frac{{2\left( {{t^2} + 1} \right) \cdot 2t \cdot t - {{\left( {{t^2} + 1} \right)}^2}}}{{{t^2}}} = \frac{{\left( {{t^2} + 1} \right)\left( {3{t^2} - 1} \right)}}{{{t^2}}}.$$所以当 $t = \dfrac{1}{{\sqrt 3 }}$ 即 $y_0=\dfrac 43$ 时，$f\left( t \right)$ 取得最小值 $\dfrac{{16\sqrt 3 }}{9}$，于是 $S$ 的最小为 $\dfrac{{8\sqrt 3 }}{9}$．
设过 $A,B$ 的切线交于点 $P$，与 $x$ 轴分别交于点 $M,N$．设 $A\left( {x_1},{y_1} \right)$，$B\left( {x_2}, {y_2} \right)$，$P\left( {x_0},{y_0} \right)$，则$${y_1} = 1 - {x_1}^2,\quad {y_2} = 1 - {x_2}^2.$$直线 $AB$：$\dfrac{{y + {y_0}}}{2} = 1 - {x_0}x$，即$$y = - 2{x_0}x + 2 - {y_0}.$$直线 $PA$：$y = - 2{x_1}x + 2 - {y_1}$，直线 $PB$：$y = - 2{x_2}x + 2 - {y_2}$．于是 $M$、$N$ 的横坐标分别为 $\dfrac{{2 - {y_1}}}{{2{x_1}}}$ 和 $\dfrac{{2 - {y_2}}}{{2{x_2}}}$．因此所围成的面积\[\begin{split}S &= \frac{1}{2} \cdot \left| {\frac{{2 - {y_2}}}{{2{x_2}}} - \frac{{2 - {y_1}}}{{2{x_1}}}} \right| \cdot {y_0} \\&= \frac{1}{2}\left| {\frac{{1 + {x_2}^2}}{{2{x_2}}} - \frac{{1 + {x_1}^2}}{{2{x_1}}}} \right| \cdot {y_0} \\&= \left| {\frac{{\left( {{x_1} - {x_2}} \right)\left( {1 - {x_1}{x_2}} \right)}}{{{x_1}{x_2}}}} \right| \cdot \frac{{{y_0}}}{4}.\end{split}\]将直线 $AB$ 与抛物线联立，有$$- 2{x_0}x + 2 - {y_0} = 1 - {x^2},$$即 ${x^2} - 2{x_0}x + 1 - {y_0} = 0$．所以$${x_1}{x_2} = 1-{y_0}, {x_1} + {x_2} = 2{x_0}.$$进而$$\left| {{x_1} - {x_2}} \right| = 2\sqrt {{x_0}^2 + {y_0} - 1} .$$于是$$S = \left| {\frac{{2\sqrt {{x_0}^2 + {y_0} - 1} \cdot {y_0}}}{{1 - {y_0}}}} \right| \cdot \frac{{{y_0}}}{4} = \frac{{{y_0}^2}}{2} \cdot \left| {\frac{{\sqrt {{x_0}^2 + {y_0} - 1} }}{{1 - {y_0}}}} \right|$$因为 ${x_1}, {x_2}$ 异号，于是 ${x_1}{x_2} < 0$，${y_0} - 1 > 0$，于是$$S = \frac{{{y_0}^2}}{{2\left( {{y_0} - 1} \right)}} \cdot \sqrt {{x_0}^2 + \left( {{y_0} - 1} \right)} \geqslant \frac{{{y_0}^2}}{{2\sqrt {{y_0} - 1} }},$$当且仅当 ${x_0} = 0$ 时取等号．设 $\sqrt {{y_0} - 1} = t$，$t > 0$，则 $S \geqslant \dfrac{{{{\left( {{t^2} + 1} \right)}^2}}}{{2t}}$ 令 $f\left( t \right) = \dfrac{{{{\left( {{t^2} + 1} \right)}^2}}}{t}$，则$$f'\left( t \right) = \frac{{2\left( {{t^2} + 1} \right) \cdot 2t \cdot t - {{\left( {{t^2} + 1} \right)}^2}}}{{{t^2}}} = \frac{{\left( {{t^2} + 1} \right)\left( {3{t^2} - 1} \right)}}{{{t^2}}}.$$所以当 $t = \dfrac{1}{{\sqrt 3 }}$ 即 $y_0=\dfrac 43$ 时，$f\left( t \right)$ 取得最小值 $\dfrac{{16\sqrt 3 }}{9}$，于是 $S$ 的最小为 $\dfrac{{8\sqrt 3 }}{9}$．
答案
解析
备注
