设函数 $f\left( x \right) = \left| {\sin x} \right| + \left| {\cos x} \right|$,试讨论 $f\left( x \right)$ 的性质(有界性、奇偶性、单调性和周期性),求其极值,并作出其在 $\left[ {0,2{\mathrm{\pi }}} \right]$ 内的图像.
【难度】
【出处】
2007年上海交通大学冬令营选拔测试
【标注】
【答案】
有界性:上(确)界为 $\sqrt 2 $,下(确)界为 $1$.
奇偶性:偶函数.
单调性:在 $\left( {\dfrac{{k{\mathrm{\pi }}}}{2},\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4}} \right)$ 上递增;在 $\left( {\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4},\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{2}} \right)$ 上递减,其中 $k \in {\mathbb{Z}}$.
周期性:最小正周期为 $\dfrac{{\mathrm{\pi }}}{2}$.
极值:在 $x = \dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4}$,$k \in {\mathbb{Z}}$ 处取得极大值 $\sqrt 2 $;在 $x = \dfrac{{k{\mathrm{\pi }}}}{2}$,$k \in {\mathbb{Z}}$ 处取得极小值 $1$.
图像: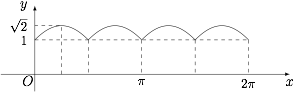
奇偶性:偶函数.
单调性:在 $\left( {\dfrac{{k{\mathrm{\pi }}}}{2},\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4}} \right)$ 上递增;在 $\left( {\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4},\dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{2}} \right)$ 上递减,其中 $k \in {\mathbb{Z}}$.
周期性:最小正周期为 $\dfrac{{\mathrm{\pi }}}{2}$.
极值:在 $x = \dfrac{{k{\mathrm{\pi }}}}{2} + \dfrac{{\mathrm{\pi }}}{4}$,$k \in {\mathbb{Z}}$ 处取得极大值 $\sqrt 2 $;在 $x = \dfrac{{k{\mathrm{\pi }}}}{2}$,$k \in {\mathbb{Z}}$ 处取得极小值 $1$.
图像:

【解析】
略.
答案
解析
备注