若函数形式为 $f\left( {x,y} \right) = a\left( x \right)b\left( y \right) + c\left( x \right)d\left( y \right)$，其中 $a\left( x \right) ,c\left( x \right)$ 为关于 $x$ 的多项式，$b\left( y \right),d\left( y \right)$ 为关于 $y$ 的多项式，则称 $f\left( {x ,y} \right)$ 为 $P$ 类函数，判断下列函数是否是 $P$ 类函数，并说明理由．
【难度】
【出处】
2006年上海交通大学推优保送生考试
【标注】
-
$1 + xy$；标注答案$1 + xy$ 为 $P$ 类函数解析设$$1 + xy = \left( {{a_1}x + {a_0}} \right)\left( {{b_1}y + {b_0}} \right) + \left( {{c_1}x + {c_0}} \right)\left( {{d_1}y + {d_0}} \right),$$则$$\begin{cases}
{a_1}{b_1} + {c_1}{d_1} = 1 ,\\
{a_1}{b_0} + {c_1}{d_0} = 0 ,\\
{a_0}{b_1} + {c_0}{d_1} = 0 ,\\
{a_0}{b_0} + {c_0}{d_0} = 1.\\
\end{cases}$$记向量 $\left( {{a_0},{c_0}} \right),\left( {{a_1},{c_1}} \right),\left( {{b_0},{d_0}} \right),\left( {{b_1},{d_1}} \right)$ 为 ${A_0},{A_1},{B_0},{B_1}$，则
${A_0} \perp {B_1},{A_1} \perp {B_0}$，且 ${A_0}$ 与 ${B_0}$、${A_1}$ 与 ${B_1}$ 成锐角或同向．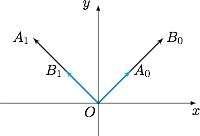
如图构造，$$1 + xy = \left( { - x + \dfrac{1}{2}} \right)\left( { - \dfrac{1}{2}y + 1} \right) + \left( {x + \dfrac{1}{2}} \right)\left( {\dfrac{1}{2}y + 1} \right),$$所以 $1 + xy$ 为 $P$ 类函数． -
$1 + xy + {x^2}{y^2}$．标注答案$1 + xy + {x^2}{y^2}$ 不是 $P$ 类函数解析设$$1 + xy + {x^2}{y^2} = \left( {{a_2}{x^2} + {a_1}x + {a_0}} \right)\left( {{b_2}{y^2} + {b_1}y + {b_0}} \right) + \left( {{c_2}{x^2} + {c_1}x + {c_0}} \right)\left( {{d_2}{y^2} + {d_1}y + {d_0}} \right),$$则 $i \ne j$ 时，$${a_i}{b_j} + {c_i}{d_j} = 0.$$当 $i = j$ 时，$${a_i}{b_i} + {c_i}{d_j} = 1,$$其中 $i,j = 0,1,2$．记向量 $\left( {{a_0},{c_0}} \right),\left( {{a_1},{c_1}} \right),\left( {{a_2},{c_2}} \right),\left( {{b_0},{d_0}} \right),\left( {{b_1},{d_1}} \right),\left( {{b_2},{d_2}} \right)$ 为 $\overrightarrow{A_0},\overrightarrow{A_1},\overrightarrow{A_2},\overrightarrow{B_0},\overrightarrow{B_1},\overrightarrow{B_2}$，则$$\overrightarrow{A_0}\cdot\overrightarrow{B_0} = \overrightarrow{A_1}\cdot\overrightarrow{B_1} = \overrightarrow{A_2}\cdot\overrightarrow{B_2} = 1.$$所以 $\overrightarrow{A_0},\overrightarrow{A_1},\overrightarrow{A_2},\overrightarrow{B_0},\overrightarrow{B_1},\overrightarrow{B_2}$ 均为非零向量．而 $\overrightarrow{A_0} \perp {B_1},{A_0} \perp {B_2}$，所以 $\overrightarrow{B_1},\overrightarrow{B_2}$ 共线，类似可证明 $\overrightarrow{B_0},\overrightarrow{B_2}$ 共线，于是 $\overrightarrow{B_0},\overrightarrow{B_1},\overrightarrow{B_2}$ 共线；同理 $\overrightarrow{A_0},\overrightarrow{A_1},\overrightarrow{A_2}$ 共线，于是 $\overrightarrow{A_0} \perp \overrightarrow{B_0}$，矛盾．
综上，$1 + xy + {x^2}{y^2}$ 不是 $P$ 类函数．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
