已知 $\triangle ABC$ 面积为 $1$，$D,E,F$ 分别在 $BC,CA,AB$ 上，$BD = 2DC$，$CE = 2EA$，$AF = 2FB$，$AD,BE,CF$ 两两相交于 $P,Q,R$．求 $\triangle PQR$ 的面积．
【难度】
【出处】
2009年中国科学技术大学自主招生保送生测试
【标注】
【答案】
$\dfrac 17$
【解析】
如图，作 $EM ,FN$ 平行于 $BC$．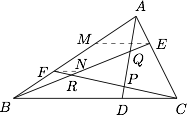
则$$EM = \dfrac{1}{3}BC, FN = \dfrac{1}{2}EM = \dfrac{1}{6}BC,$$所以$$\dfrac{{FR}}{{RC}} = \dfrac{1}{6}, {S_{\triangle BCR}} = \dfrac{6}{7}{S_{\triangle BCF}} = \dfrac{6}{7} \times \dfrac{1}{3}{S_{\triangle ABC}} = \dfrac{2}{7}.$$同理$${S_{\triangle ABQ}} = {S_{\triangle ACP}} = \dfrac{2}{7},$$因此$${S_{\triangle PQR}} = 1 - \dfrac{2}{7} \times 3 = \dfrac{1}{7}.$$
则$$EM = \dfrac{1}{3}BC, FN = \dfrac{1}{2}EM = \dfrac{1}{6}BC,$$所以$$\dfrac{{FR}}{{RC}} = \dfrac{1}{6}, {S_{\triangle BCR}} = \dfrac{6}{7}{S_{\triangle BCF}} = \dfrac{6}{7} \times \dfrac{1}{3}{S_{\triangle ABC}} = \dfrac{2}{7}.$$同理$${S_{\triangle ABQ}} = {S_{\triangle ACP}} = \dfrac{2}{7},$$因此$${S_{\triangle PQR}} = 1 - \dfrac{2}{7} \times 3 = \dfrac{1}{7}.$$
答案
解析
备注
