已知集合 $A=\{1,2,3,\cdots ,2n\}$（$n\in {\mathbb N}^+$）．对于 $A$ 的一个子集 $S$，若存在不大于 $n$ 的正整数 $m$，使得对于 $S$ 中的任意一对元素 $s_1$，$s_2$，都有 $|s_1-s_2|\ne m$，则称 $S$ 具有性质 $P$．
【难度】
【出处】
无
【标注】
-
当 $n=10$ 时，试判断集合 $B=\{x\in A\mid x>9\}$ 和 $C=\{x\in A\mid x=3k-1,k\in \mathbb N^+\}$ 是否具有性质 $P$？并说明理由．标注答案集合 $B$ 不具有性质 $P$，集合 $C$ 具有性质 $P$解析对于集合 $B$，取 $b_1=10$，则无论 $m$ 取任何不大于 $10$ 的整数值，都有$$b_2=10+m\in B,$$因此集合 $B$ 不具有性质 $P$；
对于集合 $C$，由于 $C$ 中的元素除 $3$ 的余数均为 $2$，因此其中任意两个元素的差均为 $3$ 的整数倍，因此可以取 $m=1$ 或 $m=2$，都可以说明集合 $C$ 具有性质 $P$． -
若 $n=1000$ 时，
① 若集合 $S$ 具有性质 $P$，那么集合 $T=\{2001-x\mid x\in S\}$ 是否一定具有性质 $P$？并说明理由；
② 若集合 $S$ 具有性质 $P$，求集合 $S$ 中元素个数的最大值．标注答案① 集合 $T$ 一定具有性质 $P$；② $1333$解析当 $n=1000$ 时，$$A=\{1,2,3,\cdots ,1999,2000\}.$$① 若集合 $S$ 具有性质 $P$，那么集合 $T=\{2001-x\mid x\in S\}$ 一定具有性质 $P$．
用反证法．
若 $T$ 不具有性质 $P$，则存在$$t_1,t_2\in T , m\leqslant n , m\in \mathbb N^+$$使得$$|t_1-t_2|=m.$$根据集合 $T$ 的定义，设$$t_1=2001-s_1 , t_2=2001-s_2,$$其中 $s_1,s_2\in S$，则有$$|s_1-s_2|=|(2001-s_1)-(2001-s_2)|=|t_1-t_2|=m,$$这与集合 $S$ 具有性质 $P$ 矛盾．
因此集合 $T$ 一定具有性质 $P$．
② 对于每个不大于 $n$ 的正整数 $m$，我们都可以将集合 $A$ 划分为 $A_1,A_2,\cdots ,A_m$ 共 $m$ 个同余类，其中$$A_k=\{k,m+k,2m+k,\cdots \}.$$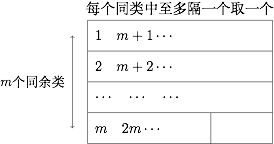
这样一来，对于集合 $A$ 中的任意两个元素 $a_1,a_2$，如果它们位于不同的同余类中，那么一定有 $|a_1-a_2|\ne m$．
因此具有性质 $P$ 的集合 $S$ 是集合 $A$ 的 $m$ 个同余类的子集的并．
下面对集合 $A_k$ 进行分析：
容易证明，从集合 $A_k$ 中选出的元素$$\dfrac{\mathrm{card}{A_k}+1}{2}\leqslant \dfrac 23 \mathrm{card}{A_k},$$于是$$\mathrm{card} S\leqslant \dfrac 23 \cdot 2n=1333\dfrac 13.$$另一方面，取 $m=667$，使得每行的利用率尽可能靠近 $\dfrac 23$．
可以构造集合$$S=\{1,2,\cdots ,667,1335,1336,\cdots ,2000\}.$$综上，集合 $S$ 中元素个数的最大值为 $1333$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
