如图,$\angle ABC=\angle ADC=90^\circ$,$\angle BAD=60^\circ$,$BC=2CD=2$,求 $AC$;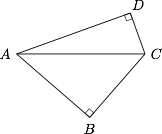

【难度】
【出处】
无
【标注】
【答案】
$\dfrac{2\sqrt{21}}3$
【解析】
连接 $BD$,因为 $A,B,C,D$ 四点共圆,$AC$ 为圆的直径.
在 $\triangle BCD$ 中,由余弦定理得$$BD=\sqrt{1^2+2^2-2\cdot 1\cdot 2\cos 120^\circ}=\sqrt 7,$$由正弦定理得$$AC=\dfrac {BD}{\sin 60^\circ}=\dfrac 23\sqrt{21}.$$
在 $\triangle BCD$ 中,由余弦定理得$$BD=\sqrt{1^2+2^2-2\cdot 1\cdot 2\cos 120^\circ}=\sqrt 7,$$由正弦定理得$$AC=\dfrac {BD}{\sin 60^\circ}=\dfrac 23\sqrt{21}.$$
答案
解析
备注