如图,已知扇形 $AOB$ 的圆心角为 $120^\circ$,$P$ 为弧 $AB$ 上一点,$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$.求 $x+y$ 的取值范围.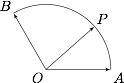

【难度】
【出处】
无
【标注】
【答案】
$[1,2]$
【解析】
不妨设扇形的半径为 $1$.根据已知条件,有$$\overrightarrow{OP}\cdot\overrightarrow{OP}=\left(x\overrightarrow{OA}+y\overrightarrow{OB}\right)\cdot\left(x\overrightarrow{OA}+y\overrightarrow{OB}\right),x,y\geqslant 0$$于是 $1=x^2-xy+y^2$,因此$$xy=\frac{(x+y)^2-1}3\leqslant \left(\frac{x+y}2\right)^2,$$解得 $x+y\leqslant 2$,等号当且仅当 $x=y=1$ 时取得.又$$(x+y)^2\geqslant x^2-xy+y^2=1,$$于是 $x+y\geqslant 1$,等号当且仅当 $xy=0$ 时取得.这样,就得到 $x+y$ 的取值范围是 $[1,2]$.
答案
解析
备注