已知直线 $l:x=t$ 与椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）相交于 $A,B$ 两点，$M$ 是椭圆 $C$ 上一点，设直线 $MA,MB$ 分别与 $x$ 轴交于 $E,F$ 两点，$O$ 为坐标原点，求证：$|OE|\cdot |OF|$ 为定值．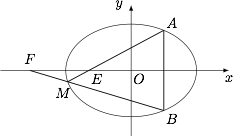
【难度】
【出处】
无
【标注】
【答案】
定值为 $a^2$
【解析】
利用仿射变换 $x'=x$，$y'=\dfrac ab y$ 将椭圆 $C$ 变为圆 $C':x'^2+y'^2=a^2$，如图．
由于 $\angle OMB=\angle OBM=\angle OAF$，于是 $O,M,F,A$ 四点共圆，进而有\[\angle OMA=\angle AFO=\angle MFO,\]因此 $\triangle OME$ 与 $\triangle OFM$ 相似，进而\[|OE|\cdot |OF|=|OM|^2=a^2\]为定值．
由于 $\angle OMB=\angle OBM=\angle OAF$，于是 $O,M,F,A$ 四点共圆，进而有\[\angle OMA=\angle AFO=\angle MFO,\]因此 $\triangle OME$ 与 $\triangle OFM$ 相似，进而\[|OE|\cdot |OF|=|OM|^2=a^2\]为定值．
答案
解析
备注
