已知 $x>0$，求证：$\left( \mathrm{e}^x-1\right)\cdot \ln (1+x)>x^2 $．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图．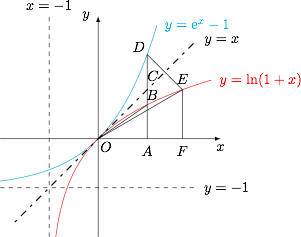
取点 $A(x,0)(x>0)$，作直线 $l$ 与 $x$ 轴垂直，分别交函数 $y=\ln{(1+x)},y=x,y=\mathrm{e} ^x-1$ 的图象于点 $B,C,D$，设点 $E$ 与点 $D$ 关于直线 $y=x$ 对称，则要证的结论等价于$$\left|AD\right|\cdot\left|AB\right|>\left|AC\right|^2.$$由于函数 $y=\ln{(1+x)}$ 在其定义域 $\left(-1,+\infty\right) $ 上凹，故$$\dfrac{\left|AB\right|}{\left|AC\right|}=\dfrac{\left|AB\right|}{\left|AO\right|} =\tan{\angle AOB}>\tan{\angle EOF}=\dfrac{\left|EF\right|}{\left|OF\right|}=\dfrac{\left|AC\right|}{\left|AD\right|},$$所以要证的结论成立．
取点 $A(x,0)(x>0)$，作直线 $l$ 与 $x$ 轴垂直，分别交函数 $y=\ln{(1+x)},y=x,y=\mathrm{e} ^x-1$ 的图象于点 $B,C,D$，设点 $E$ 与点 $D$ 关于直线 $y=x$ 对称，则要证的结论等价于$$\left|AD\right|\cdot\left|AB\right|>\left|AC\right|^2.$$由于函数 $y=\ln{(1+x)}$ 在其定义域 $\left(-1,+\infty\right) $ 上凹，故$$\dfrac{\left|AB\right|}{\left|AC\right|}=\dfrac{\left|AB\right|}{\left|AO\right|} =\tan{\angle AOB}>\tan{\angle EOF}=\dfrac{\left|EF\right|}{\left|OF\right|}=\dfrac{\left|AC\right|}{\left|AD\right|},$$所以要证的结论成立．
答案
解析
备注
