如图,在直三棱柱 $ABC-A_{1}B_{1}C_{1}$ 中,$\angle BAC=90^{\circ}$,$AB=a$,$AC=2$,$AA_{1}=1$.点 $D$ 在棱 $B_{1}C_{1}$ 上,且 $B_{1}D:DC_{1}=1:3$.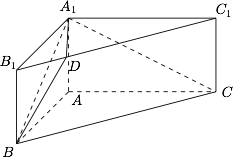

【难度】
【出处】
2013年全国高中数学联赛河北省预赛
【标注】
-
证明:$BD\perp A_{1}C$;标注答案略解析作 $DE\parallel A_{1}B_{1}$ 交 $A_{1}C_{1}$ 于 $E$,则$$DE\perp A_{1}C_{1}.$$因为 $ABC-A_{1}B_{1}C_{1}$ 为直三棱柱,
所以$$\text{平面 }A_{1}B_{1}C_{1}\perp \text{平面}A_{1}C,$$故$$DE\perp \text{平面}A_{1}C.$$连结 $AE$,则 $AE$ 为 $BD$ 在平面 $A_{1}C$ 的射影,在矩形 $A_{1}C_{1}CA$ 中,计算可得$$AE\perp A_{1}C,$$由三垂线定理得$$BD\perp A_{1}C.$$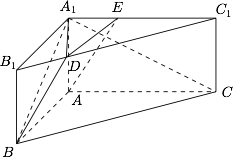
-
当 $a$ 为何值时,二面角 $B-A_{1}D-B_{1}$ 的大小为 $60^{\circ}$?标注答案$\dfrac{2\sqrt 3}{3}$解析作 $B_{1}F\perp A_{1}D$,垂足为 $F$,连 $BF$,则$$BF\perp A_{1}D,$$所以 $\angle BFB_{1}$ 为二面角 $B-A_{1}D-B_{1}$ 的平面角,故$$\angle BFB_{1}=60^{\circ} , B_{1}F=\dfrac{\sqrt 3}{3},$$所以\[A_{1}D=\sqrt{A_{1}E^{2}+DE^{2}}=\dfrac{\sqrt{9a^{2}+4}}{4}.\]因为 $S_{\triangle A_{1}B_{1}D}=\dfrac{1}{4}S_{\triangle A_{1}B_{1}C_{1}}=\dfrac{a}{4}$,所以\[\dfrac{1}{2}\cdot A_{1}D\cdot B_{1}F=\dfrac{1}{2}\cdot \dfrac{\sqrt{9a^{2}+4}}{4}\cdot \dfrac{\sqrt 3}{3}=\dfrac{a}{4},\]解得 $a=\dfrac{2\sqrt3}{3}$.
因此当 $a=\dfrac{2\sqrt 3}{3}$ 时,二面角 $B-A_{1}D-B_{1}$ 为 $60^{\circ}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2