在如图所示的几何体中,$EA\perp$ 平面 $ABC$,$DB\perp $ 平面 $ABC$,$AC\perp BC$,且 $BC=BD=\dfrac 32 AE=a$,$AC=\sqrt 2 a$,$AM=2MB$.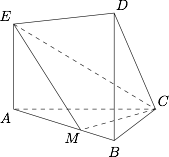

【难度】
【出处】
2011年全国高中数学联赛黑龙江省预赛
【标注】
-
求证:$CM\perp EM$;标注答案略解析因为$$BC=a,AC=\sqrt 2 a,AC\perp BC,$$所以$$AB=\sqrt 3 a.$$过 $C$ 作 $CM'\perp AB$ 交 $AB$ 于 $M'$,则$$BC^2=BM'\cdot BA,$$所以$$BM'=\dfrac{\sqrt 3}{3}a.$$因此$$AM'=2M'B,$$故 $M$ 与 $M'$ 重合,所以$$CM\perp AB.$$又因为 $EA\perp $ 平面 $ABC$,$CM\subset $ 平面 $ABC$,所以$$CM\perp EA.$$因为 $EA\cap AB=A$,所以 $CM\perp$ 平面 $EABD$,从而 $CM\perp EM$.
-
求直线 $CD$ 与平面 $MCE$ 所成角的大小.标注答案$\arcsin{\dfrac{\sqrt 6}{3}}$解析又因为 $CM\subset $ 平面 $EMC$,所以平面 $EMC\perp $ 平面 $EABD$,且平面 $EMC\cap $ 平面 $EABD=EM$.
过 $D$ 作 $DF\perp EM$ 交 $EM$ 于 $F$,则 $DF\perp $ 平面 $EMC$.
连接 $FC$,则 $\angle{DCF}$ 为 $CD$ 与平面 $MCE$ 所成的角.
用等面积法计算得$$DF=\dfrac{2\sqrt 3}{3}a,$$因此$$\sin{\angle{DCF}}=\dfrac {DF}{CD}=\dfrac{\sqrt 6}{3},$$故 $\angle{DCF}=\arcsin {\dfrac{\sqrt 6}{3}}$.
所以直线 $CD$ 与平面 $MCE$ 所成角的大小为 $\arcsin{\dfrac{\sqrt 6}{3}}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2