如图所示,在长方体 $ABCD-A_{1}B_{1}C_{1}D_{1}$ 中,已知 $AD=1$,$AB=2$,$AA_{1}=c$,若对角线 $BD_{1}$ 上存在一点 $P$ 使得 $PB_{1}\perp PC_{1}$,求 $c$ 的取值范围.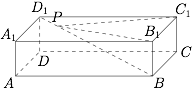

【难度】
【出处】
2013年全国高中数学联赛山东省预赛
【标注】
【答案】
$\left(0,\dfrac{1}{4}\right]$
【解析】
以 $D$ 为原点,分别以 $\overrightarrow{DA}$,$\overrightarrow{DC}$,$\overrightarrow{DD_{1}}$ 作为 $x$,$y$,$z$ 轴正向,建立空间直角坐标系,则 $B(1,2,0)$,$B_{1}(1,2,c)$,$C_{1}(0,2,c)$,$D_{1}(0,0,c)$.
设 $\overrightarrow{D_{1}P}=\lambda \overrightarrow{D_{1}B}=(\lambda ,2\lambda ,-c\lambda)$,则\[\overrightarrow{PC_{1}}=(-\lambda ,2-2\lambda ,c\lambda),\overrightarrow{PB_{1}}=(1-\lambda,2-2\lambda ,c\lambda),\]由此得\[\overrightarrow{PC_{1}}\cdot \overrightarrow{PB_{1}}=-\lambda (1-\lambda)+(2-2\lambda)^{2}+c^{2}\lambda^{2}=(c^{2}+5)\lambda^{2}-9\lambda+4=0,\]所以\[\Delta=81-16(c^{2}+5)=1-16c^{2}\geqslant 0,\]解得 $0<c\leqslant \dfrac{1}{4}$.
设 $\overrightarrow{D_{1}P}=\lambda \overrightarrow{D_{1}B}=(\lambda ,2\lambda ,-c\lambda)$,则\[\overrightarrow{PC_{1}}=(-\lambda ,2-2\lambda ,c\lambda),\overrightarrow{PB_{1}}=(1-\lambda,2-2\lambda ,c\lambda),\]由此得\[\overrightarrow{PC_{1}}\cdot \overrightarrow{PB_{1}}=-\lambda (1-\lambda)+(2-2\lambda)^{2}+c^{2}\lambda^{2}=(c^{2}+5)\lambda^{2}-9\lambda+4=0,\]所以\[\Delta=81-16(c^{2}+5)=1-16c^{2}\geqslant 0,\]解得 $0<c\leqslant \dfrac{1}{4}$.
答案
解析
备注